Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
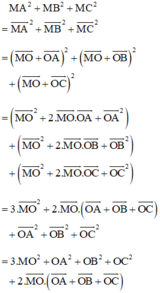
Lại có:
+ O là trọng tâm tam giác nên 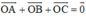
+ Bán kính đường tròn ngoại tiếp tam giác:
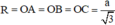
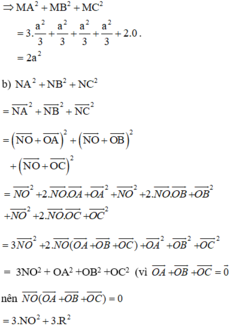
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.

Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)

Gọi O là tâm đường tròn ngoại tiếp tam giác, D là trung điểm BC
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}\)
Đặt \(T=MB^2+MC^2-2MA^2\)
\(T=\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OC}\right)^2-2\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2\)
\(=OB^2+OC^2-2OA^2+2\overrightarrow{MO}\left(\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}\right)\)
\(=2\overrightarrow{MO}\left(\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}\right)\)
\(=2\overrightarrow{MO}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=4\overrightarrow{MO}.\overrightarrow{AD}\)
\(=4R.AD.cos\left(\overrightarrow{MO};\overrightarrow{AD}\right)\)
Do R và AD cố định \(\Rightarrow T_{min}\) khi \(cos\left(\overrightarrow{MO};\overrightarrow{AD}\right)\) đạt min
\(\Rightarrow cos\left(\overrightarrow{MO};\overrightarrow{AD}\right)=-1\)
\(\Rightarrow\overrightarrow{MO}\) và \(\overrightarrow{AD}\) là 2 vecto ngược chiều
\(\Rightarrow\) M là giao điểm của đường thẳng d và đường tròn ngoại tiếp tam giác, với d đi qua O và song song AD sao cho A và M nằm về 2 phía so với đường thẳng BC

Chọn D.
Gọi điểm M có tọa độ là ( x; y)
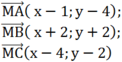
MA2 + 2MB2 + 3MC2
= (x - 1)2 + (y - 4)2 + 2[ (x + 2)2 + (y + 2)2] + 3[ (x - 4)2 + (y - 2)2]
= 6x2-18x + 6y2 + 93 = 1,5. (2x - 3)2 + 6(y - 1)2 + 147/2 ≥ 147/2
Dấu “=” xảy ra khi x = 1,5 và y = 1
Vậy tọa độ điểm M cần tìm là ( 1,5; 1).
Gọi cạnh tam giác là a thì \(a=R\sqrt{3}\)
Do tính đối xứng của đường tròn và tam giác đều, không mất tính tổng quát, giả sử M nằm trên cung nhỏ BC
\(\Rightarrow\widehat{BMC}=180^0-\widehat{BAC}=120^0\)
\(\Rightarrow AM.BC=AB.CM+AC.BM\Leftrightarrow AM=BM+CM\)
\(\Rightarrow S=\left(BM+CM\right)^2+2BM^2-3CM^2\)
\(=3BM^2+2BM.CM-2CM^2\)
Lại có: \(BC^2=BM^2+CM^2-2MB.MC.cos\widehat{BMC}\)
\(=BM^2+CM^2+MB.MC\Rightarrow MB.MC=3R^2-BM^2-CM^2\)
\(\Rightarrow S=6R^2+BM^2-4CM^2\)
Gọi I là điểm thỏa mãn \(\overrightarrow{BI}-4\overrightarrow{CI}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BI}=\dfrac{4}{3}\overrightarrow{BC}\)
\(\Rightarrow BI=\dfrac{4\sqrt{3}}{3}R\) ; \(CI=\dfrac{\sqrt{3}}{3}R\)
\(S=6R^2+\left(\overrightarrow{BI}+\overrightarrow{IM}\right)^2-4\left(\overrightarrow{CI}+\overrightarrow{IM}\right)^2\)
\(S=6R^2+BI^2-4CI^2-3IM^2=10R^2-3IM^2\)
\(S_{max}\) khi \(IM_{min}\Rightarrow M\equiv C\Rightarrow S=CA^2+2CB^2=9R^2\)
Không có đáp án thầy ạ !