Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì GM = 1/2 GB (gt)
Mà GB = GD ( G là trung điểm của BD ) nên GM = 1/2 GD
Và M là trung điểm của GD nên CM là đường trung tuyến
Ta có 2 trung tuyến CM và GE cắt nhau tại I nên I là trọng tâm của tam giác CGD

Câu 1:
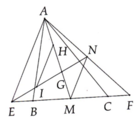
a, Vì AD là trung tuyến \(\Rightarrow AG=\frac{2}{3}AD\)\(\Rightarrow GD=\frac{1}{3}AD\)\(\Rightarrow GM=\frac{2}{3}AD\)(D là trung điểm MG)
\(\Rightarrow AG=GM\)
Vì BE là trung tuyến \(\Rightarrow BG=\frac{2}{3}BE\)\(\Rightarrow GE=\frac{1}{3}BE\)\(\Rightarrow GN=\frac{2}{3}BE\)(E là trung điểm GN)
\(\Rightarrow BG=GN\)
b, Xét △ANG và △MBG
Có: AG = MG (cmt)
AGN = MGB (2 góc đối đỉnh)
NG = BG (cmt)
=> △ANG = △MBG (c.g.c)
=> AN = MB (2 cạnh tương ứng)
và ANG = MBG (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AN // MB (dhnb)
Câu 2: sai đề???

1:
Xét ΔBAC có
BM,CN là trung tuyến
BM cắt CN tại G
=>G là trọng tâm
=>BG=2/3BM và CG=2/3CN
BG+CG>BC
=>2/3BM+2/3CN>BC
=>2/3(BM+CN)>BC
=>BM+CN>3/2BC
2:
BF=2BE
=>EF=BE
=>EF=2ED
=>D là trung điểm của EF
Xét ΔFEC có
CD,EK là trung tuyến
CD cắt EK tại G
=>G là trọng tâm
b: G là trọng tâm của ΔFEC
=>GE/GK=1/2 và GC/DC=2