Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A,B,D,C cùng thuộc (O)
=>ABDC nọi tiép
b: AB vuông góc BD
=>AB là tiếp tuyến của (D)
AC vuông góc CD
=>AC là tiếp tuyến của (D)
MB,MF là tiêp tuyến của (D) nên MB=MF
NF,NC là tiếp tuyến của (D) nên NF=NC
=>BM+NC=MF+NF=MN

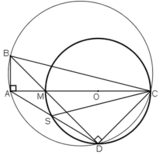
a) 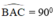 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC

⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
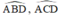 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 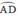
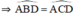
c) + Trong đường tròn đường kính MC:
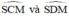 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 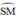
+ Trong đường tròn đường kính BC:
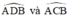 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 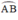
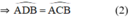


a: Vì A,B,D,C cùng nằm trên (O)
nên ABDC nội tiếp
b: Xét (D) có
MB,MF là tiếp tuyến
=>MB=MF
Xét (D) có
NF,NC là tiếp tuyến
=>NF=NC
=>MB+CN=MF+NF=MN
a: góc CDM=1/2*sđ cung CM=90 độ
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
c: Gọi F là giao của AB và CD
góc MEC=1/2*sđ cung MC=90 độ
=>ME vuông góc CB(1)
Xet ΔFCB có
CA,BD là đường cao
CA cắt BD tại M
=>M là trực tâm
=>FM vuông góc BC(2)
Từ (1), (2) suy ra F,M,E thẳng hàng