K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2021
2: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBDC vuông tại B có BA là đường cao ứng với cạnh huyền DC
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)
10 tháng 8 2016
Bạn tự vẽ hình :)
a) Ta có : AB = Cos 60 . BC = 1/2 . 12 = 6 cm
AC = Sin 60 . BC = \(\frac{\sqrt{3}}{2}.12=6\sqrt{3}\)
b) BE là tia p/g góc B nên ta có góc ABE = góc EBC = 30 độ
AE = tan 30 . AB = ...
BH = Cos 60. AB = ....
Suy ra AE . AC =BH.BC (bạn tự thay số vào tính)
c) Hãy chứng minh D là trung điểm AH
Sau đó áp dụng tính chất đường trung bình để suy ra DM , DN , MN song song với BC và áp dụng tiên đề Ơ-Clit là ra :)
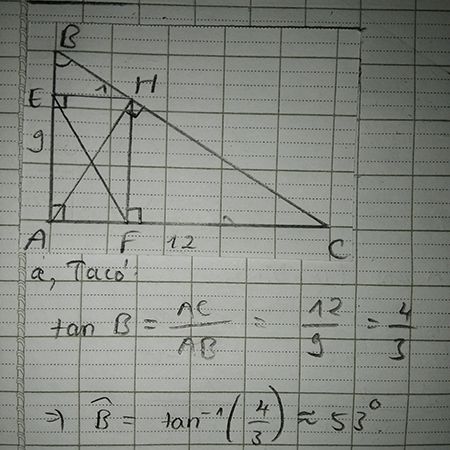
Giúp mik câu c với ạ
a: BC=15cm
AH=7,2cm