Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

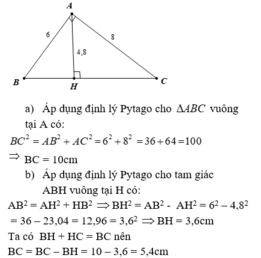
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(cạnh huyền-góc nhọn)
c) Ta có: ΔADH vuông tại H(gt)
nên \(\widehat{HDA}+\widehat{HAD}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BDA}+\widehat{HAD}=90^0\)(2)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)(tia AD nằm giữa hai tia AB,AC)
nên \(\widehat{BAD}+\widehat{KAD}=90^0\)(3)
Từ (2) và (3) suy ra \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔBAD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔBAD cân tại B(Định lí đảo của tam giác cân)

a) bạn tự vẽ hình nhé
sau khi kẻ, ta có AC=AH+HC=11
mà tam giác ABH vuông tại H
=> theo định lý Pytago => AH^2+BH^2=AB^2
=>BH=căn bậc 2 của 57
cũng theo định lý Pytago
=>BC^2=HC^2+BH^2
=>BC=căn bậc 2 của 66
b) bạn tự vẽ hình tiếp nha
ta có M là trung điểm của tam giác ABC => AM là đường trung tuyến của tam giác ABC vuông tại A
=>AM=MB=MC
theo định lý Pytago =>do tam giác HAM vuông tại H
=>HM^2+HA^2=AM^2
=>HM=9 => HB=MB-MH=32
=>AB^2=AH^2+HB^2 =>AB=căn bậc 2 của 2624
tương tự tính được AC=căn bậc 2 của 4100
=> AC/AB=5/4
CHÚC BẠN HỌC TỐT!!!

a) Áp dụng ĐL Pytago ta có: \(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
b) Xét \(\Delta ABH\) và \(\Delta ADH\) có:
\(AH\) chung
\(\widehat{AHB}=\widehat{AHD}=90^0\)
\(BH=DH\) (gt)
\(\Rightarrow\Delta ABH=\Delta ADH\left(c.g.c\right)\)
c) Do \(\Delta ABH=\Delta ADH\Rightarrow\widehat{B}=\widehat{ADH}\) mà \(\widehat{ADH}=\widehat{EDC}\) (đối đỉnh)
\(\Rightarrow\widehat{EDC}=\widehat{B}\)
Lại có \(BA//DK\) (do cùng vuông góc \(AC\)) \(\Rightarrow\widehat{KDC}=\widehat{B}\) (đồng vị)
Xét \(\Delta DKC\) và \(\Delta DEC\) có:
\(\widehat{DKC}=\widehat{DEC}=90^0\)
\(CD\) chung
\(\widehat{KDC}=\widehat{EDC}=\widehat{B}\)
\(\Rightarrow\Delta DKC=\Delta DEC\) (ch - gn) \(\Rightarrow DE=DK\)
d) Xét tam giác \(AMC\) có: \(\left\{{}\begin{matrix}MK\perp AC\\AE\perp MC\\MK\cap AE=D\end{matrix}\right.\)
\(\Rightarrow D\) là trực tâm \(\Rightarrow MD\perp AC\) mà \(DK\perp AC\Rightarrow MD\equiv MK\)
\(\Rightarrow MK\perp AC\Rightarrow MK//AB\)

a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAK vuông tại A và ΔBIK vuông tại I có
BK chung
góc ABK=góc IBK
=>ΔBAK=ΔBIK
=>KA=KI
c: góc DAI+góc BIA=90 độ
góc CAI+góc BAI=90 độ
mà góc BIA=góc BAI
nên góc DAI=góc CAI
=>AI là phân giác của góc DAC