Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
+) \(\Delta\)ABC vuông tại A
theo định lí pitago => \(BC=\sqrt{AB^2+AC^2}=13\)
+) BF là tia phân giác ^ABC
Theo tích chất phân giác: \(\frac{AF}{CF}=\frac{AB}{CB}=\frac{5}{13}\)
=> \(\frac{AF}{5}=\frac{CF}{13}=\frac{AF+CF}{5+13}=\frac{12}{18}=\frac{2}{3}\)
=> AF = 10/3 và CF = 26/3
b) Xét \(\Delta\)ABF và \(\Delta\)HBE có: ^ABF = ^HBE ( tích chất phân giác ) và ^FAB = ^EHB = 90 độ
=> \(\Delta\)ABF ~ \(\Delta\)HBE
c) (b) => ^BEH = ^BFA mà ^BEH = ^AEF ( đối đỉnh)
=> ^AEF = ^BFA = ^EFA
=> \(\Delta\)AEF cân
BC). Tia phân giác của góc ABC cắt AH tại E và cắt AC tại F.
4:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b Xét ΔABC vuông tại A có AH là đường cao
nen AH^2=HB*HC
c: BC=căn 6^2+8^2=10(cm)
=>AH=6*8/10=4,8cm
a: BC=căn 6^2+8^2=10cm
BF là phân giác
=>FA/AB=FC/BC
=>FA/3=FC/5=(FA+FC)/(3+5)=8/8=1
=>FA=3cm; FC=5cm
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
2)
b) theo câu a thì ta có góc BEH = góc AFB
mà góc BEH = góc AEF
\(\Rightarrow\) Tam giác AEF cân tại A
c) Xét tam giác ABH có BE là tia phân giác của góc ABH
\(\Rightarrow\frac{EH}{EA}=\frac{BH}{BA}\) (1)
lại có tam giác ABH đồng dạng vs tam giác CBA ( g.g )
\(\Rightarrow\frac{BH}{BA}=\frac{BA}{BC}\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\frac{EH}{EA}=\frac{BA}{BC}\left(=\frac{BH}{BA}\right)\) (3)
Có : BF là tia phân giác của tam giác ABC
\(\Rightarrow\) \(\frac{BA}{BC}=\frac{FA}{FC}\) (4)
Từ (3) và (4) \(\Rightarrow\frac{EH}{EA}=\frac{FA}{FC}\) \(\Leftrightarrow\) \(EH.FC=FA.EA\)
1) BC =13 ;AH=4,615384615
2a) Xét tam giác ABF và HBE có
BAF=BHE(góc vuông|)
ABF=HBE(BF là phân giác)
CÒN LẠI MIK CHỊU SORRY NHA
a, Xét tam giác ABC và tam giác HBA ta có :
^BAC = ^AHB = 900
^B _ chung
Vậy tam giác ABC ~ tam giác HBA ( g.g )
c, tam giác ABC vuông tại A, có đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64=100\Rightarrow BC=10\)cm
Ta có : \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\)( cặp tỉ số đồng dạng ý a )
\(\Rightarrow\dfrac{8}{AH}=\dfrac{10}{6}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}\)cm
d, phải là cắt AC nhé, xem lại đề nhé bạn
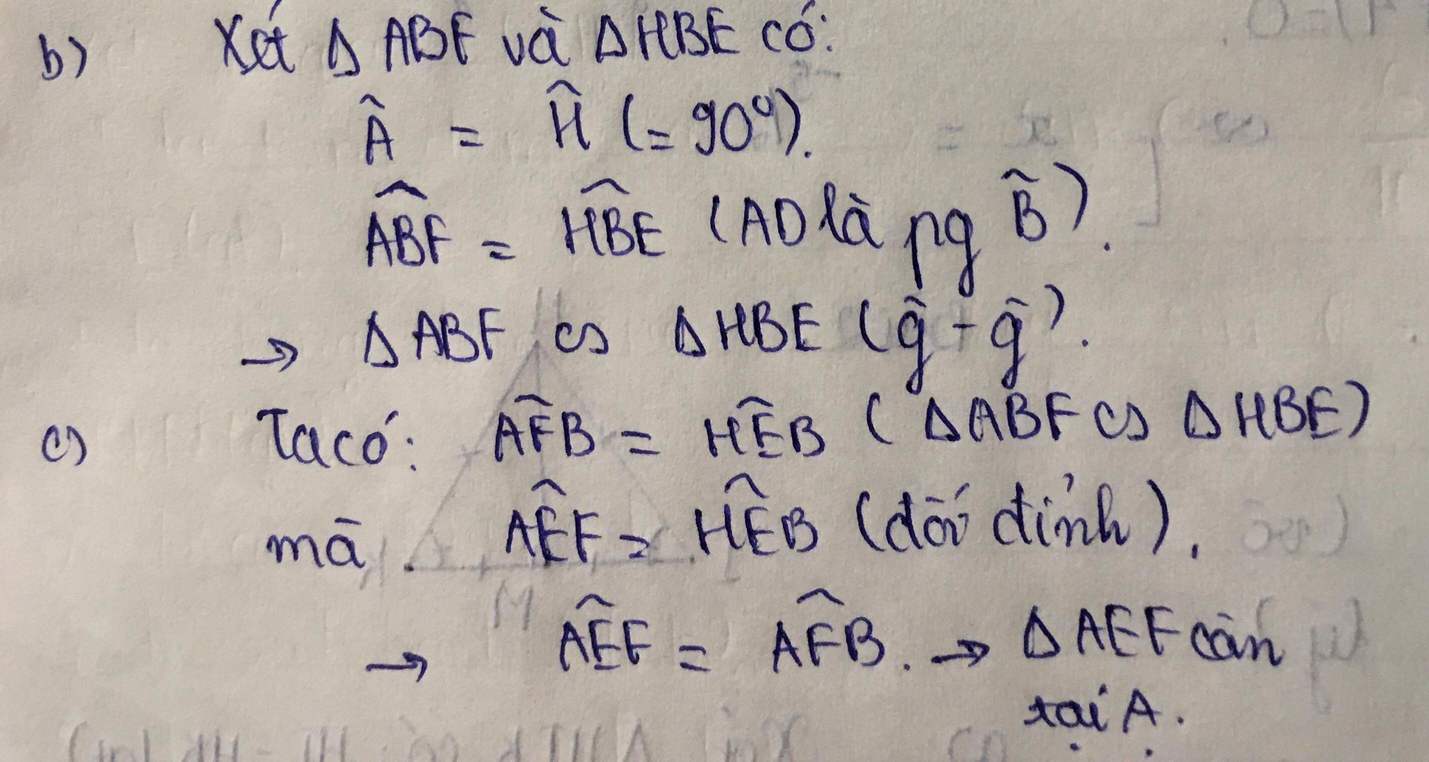
a)Xét △ABC vuông tại A (gt)
=> BC2 = AB2 + AC2 (định lý Pytago)
BC2 = 52 + 122 = 25 + 144 = 169
=> BC = \(\sqrt{169}\) = 13 cm
Xét △ABC có BF là tia phân giác của góc ABC (gt)
=>\(\dfrac{AF}{AB}\) = \(\dfrac{FC}{BC}\) (tính chất đường phân giác)
=>\(\dfrac{AF}{5}\) = \(\dfrac{FC}{13}\) và AF + FC = AC = 12
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{AF}{5}\) = \(\dfrac{FC}{13}\) = \(\dfrac{AF+FC}{5+13}\) = \(\dfrac{AC}{18}\) = \(\dfrac{2}{3}\)
=> AF = \(\dfrac{2}{3}\) x 5 = 3,33 cm và FC = \(\dfrac{2}{3}\) x 13 = 8,67 cm
b)Xét △ABF và △HBE có:
góc ABF bằng góc HBE (BF là tia phân giác của góc ABC)
góc BAF bằng góc BHE bằng 90o (tam giác ABC vuông tại A và AH ⊥ BC)
=> △ABF ∼ △HBE (g.g)
c) Vì △ABF ∼ △HBE (câu b)
=> góc BFA bằng góc BEH
mà góc AEF bằng góc BEH (2 góc đối đỉnh)
=> góc BFA bằng góc AEF
=> △AEF cân tại A
d)Xét △ABC và △AHB có:
góc ABC chung
góc BAC bằng góc BHA bằng 90o (tam giác ABC vuông tại A và AH ⊥ BC)
=> △ABC ∼ △HBA (g.g)
=> \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (1)
Xét △ABH có BE là tia phân giác của góc ABC (gt)
=>\(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (2) (tính chất đường phân giác)
Từ (1), (2) => \(\dfrac{AB}{BC}\) = \(\dfrac{HE}{AE}\)
=> AB.AE=BC.HE(chắc vậy?)
câu d sai đề à????