Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình. Gợi ý:
- Chứng minh tứ giác AEHF là hình chữ nhật.
*Gọi K là giao điểm của AH và EF. Khi đó K là trung điểm AH.
- Chứng minh tam giác AHM cân tại A. Suy ra \(\widehat{MAB}=\widehat{HAB}\)
Mặt khác \(\widehat{HAB}=\widehat{ABI}\) (BI//AH) \(\Rightarrow\widehat{MAB}=\widehat{ABI}\)
\(\Rightarrow\)△ABI cân tại I nên AI=BI.
*CA cắt BI tại S. Chứng minh I là trung điểm BS.
Đến đây bài toán đã trở nên đơn giản hơn (chỉ chú ý vào các điểm C,A,H,B,S và K).
- CK cắt BS tại I'. Khi đó ta cũng c/m được I' là trung điểm BS.
\(\Rightarrow I\equiv I'\) nên C,K,I thẳng hàng.
Suy ra đpcm.

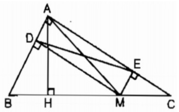
Xét tứ giác ADME, ta có:
∠ A = 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (MDA ) = 90 0
ME ⊥ AC (gt)
⇒ ∠ (MEA ) = 90 0
Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)
⇒ AM = DE ( tính chất hình chữ nhật)

Ta có AB vuông góc với AC, MF vuông góc với AC suy ra MF song song với AB, xét tam giácBca có m là trung điểm của BC, MF song song với AB suy ra ra f là trung điểm của AC mà f là trung điểm của mn suy ra m n cắt AC tại f suy ra tứ giác mcna là hình bình hành
a) Xét tứ giác AEMF có
\(\widehat{AFM}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{FAE}=90^0\)(gt)
Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AM=EF(Hai đường chéo của hình chữ nhật AFME)
b) Gọi O là giao điểm của AM và EF
Ta có: AMFE là hình chữ nhật(cmt)
nên Hai đường chéo AM và EF cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)
mà O là giao điểm của AM và EF(gt)
nên O là trung điểm của AM; O là trung điểm của EF
Ta có: ΔAHM vuông tại H(gt)
mà HO là đường trung tuyến ứng với cạnh huyền AM(O là trung điểm của AM)
nên \(HO=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà AM=EF(cmt)
nên \(HO=\dfrac{EF}{2}\)
Xét ΔHFE có
HO là đường trung tuyến ứng với cạnh EF(O là trung điểm của EF)
\(HO=\dfrac{EF}{2}\)(cmt)
Do đó: ΔHFE vuông tại H(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)