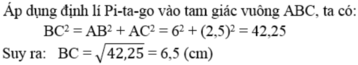
Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α Biết tg α = 5/12 . Hãy tính: Cạnh BC

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

12 tháng 11 2018

Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α

Biết tg α = 5/12 . Hãy tính: Cạnh BC

#Toán lớp 9

Cao Minh Tâm

12 tháng 11 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

31 tháng 12 2019

Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α

Biết tg α = 5/12 . Hãy tính: Cạnh AC

#Toán lớp 9

Cao Minh Tâm

31 tháng 12 2019

Đúng(0)

Bảo Minh Khôi Đàm

9 tháng 10 2021

cho tam giác ABC vuông tại A , AB = 6cm , góc B=a

biết tga=5/12 , hãy tính

a) cạnh AC

b) cạnh bc

#Toán lớp 9

Nguyễn Hoàng Minh

9 tháng 10 2021

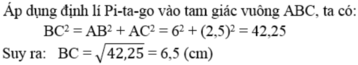
\(a,\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{5}{12}\Leftrightarrow AC=\dfrac{5}{12}\cdot6=2,5\left(cm\right)\\ b,BC=\sqrt{AC^2+AB^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\left(pytago\right)\)

Đúng(1)

Lấp La Lấp Lánh

9 tháng 10 2021

a) Xét tam giác ABC vuông tại A:

\(AC=tan\alpha.AB=\dfrac{5}{12}.6=2,5\left(cm\right)\)

b) Áp dụng đ/lý Pytago trong tam giác ABC vuông tại A:

\(BC^2=AB^2+AC^2\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{2,5^2+6^2}=6,5\left(cm\right)\)

Đúng(1)

Pham Trong Bach

7 tháng 8 2017

Cho tam giác ABC cân tại A, đường cao BH. Hãy tính góc A và các cạnh AB, BC, nếu biết BH = h, ∠ C = α

#Toán lớp 9

Cao Minh Tâm

7 tháng 8 2017

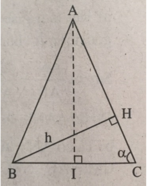
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

∠ A = 180 ° - 2 α . Tam giác vuông HBC có BC = h/sinα. Kẻ đường cao AI của tam giác ABC thì được

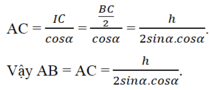
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)

NT Ánh

24 tháng 9 2016

Cho tam giác ABC vuông tại A ,AB=6cm,góc B=a

Biết tga=\(\frac{5}{12}\)hãy tính:

a) Cạnh AC

b) Cạnh BC

#Toán lớp 9

Vũ Đức Toàn

27 tháng 9 2016

a, theo đề ta có : \(\frac{AC}{AB}\) = \(\frac{5}{12}\)

=> AC= 6.5:12=2,5

b, ta có: BC= \(\sqrt{AC^2+AB^2}\) = \(\frac{13}{2}\)

Đúng(0)

Pham Trong Bach

6 tháng 2 2019

Cho tam giác ABC vuông tại A. Biết AB = 30cm, sinB = α, tanα = 5 12 . Tính cạnh BC và AC

#Toán lớp 9

Cao Minh Tâm

6 tháng 2 2019

HS tự làm

Đúng(0)

PhạM Thị Thu Trang

16 tháng 8 2017 - olm

Cho tam giác ABC vuông tại A, AB=6CM,góc B bằng a. biết tga=5/12,tính các cạnh ACvà BC

ai biết giúp mình với !!!!!!

#Toán lớp 9

Đỗ Cao Thắng

16 tháng 8 2017

AC= 2.5 BC= 5.5

Đúng(0)

Haise Ken

21 tháng 10 2018 - olm

Cho tam giác ABC vuông tại A đặt AB= c; AC=b. Gọi M là điểm tùy ý trên cạnh BC sao cho góc MAB = α (0< α<90)

CM: AM=\(\frac{bc}{b.cos\text{ }\text{α}+c.sin\text{α}}\)

#Toán lớp 9

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP