K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
18 tháng 12 2019
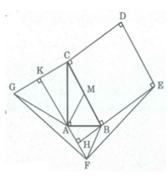
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
ABC vuông ở A (AB < AC ), đường cao AH. Gọi D là điểm đối xứng của A qua H. Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt ở M và N. Chứng minh:
CD .
11 tháng 1 2022
Bài 6:
a: Xét tứ giác AKDH có
\(\widehat{AKD}=\widehat{AHD}=\widehat{KAH}=90^0\)
Do đó: AKDH là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=BC/2=2,5(cm)
DT
11 tháng 1 2022
a. Tứ giác AKDH là hình chữ nhật , vì có góc \(DKA=KAH=DHA=90^o\)
b, áp dụng đl pytago vào tam giác vuông ABC có :
\(BC^2=AB^2+AC^2\Leftrightarrow BC=\sqrt{4^2+3^2}=5cm\)
vì AD là trung tuyến tam giác vuông ABC nên :
\(AD=\dfrac{1}{2}BC=\dfrac{1}{2}.5=2,5cm\)
c,vì AKDH là hình chữ nhật nên : DH//KA
mà D là trung điểm BC
=>H là trung điểm AC
<=>AH=\(\dfrac{1}{2}AC=\dfrac{1}{2}.3=1,5cm\)
vì AH = 1,5 cm nên => KD cũng = 1,5cm (AKDH là hình chữ nhật)
\(S_{ABD}=\dfrac{1}{2}.AB.KD=\dfrac{1}{2}.4.1,5=3cm^2\)
28 tháng 4 2023
a:
Sửa đề tam giác DEC
Xet ΔABC vuông tại A và ΔDEC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDEC
b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)
\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)
AD là phân giác
=>BD/AB=CD/AC
=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)
=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)
CM
17 tháng 10 2017
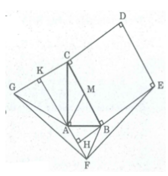
S B C D E = B C 2 = 2 a 2 = 4 a 2 (dvdt)
Trong tam giác vuông BHA, theo Pi-ta-go, ta có: A H 2 + B H 2 = A B 2
⇒ B H 2 = A B 2 - A H 2 = a 2 - a 2 / 4 = 3 a 2 / 4 ⇒ BH = (a 3 )/2
S
A
B
F
= 1/2 BH.FA =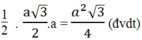 
Trong tam giác vuông AKG, theo Pi-ta-go, ta có: A C 2 = A K 2 + K C 2
⇒ A K 2 = A C 2 - K C 2 = 3 a 2 - 3 a 2 / 4 = 9 a 2 / 4 ⇒ AK = 3a/2 (đvdt)
S
A
C
G
= 1/2 AK.CG =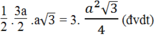 
S D E F G = S B C D E + S F B E + S FAB + S F A G + S A C G + S A B C
AH
Akai Haruma
Giáo viên
22 tháng 2 2021
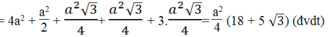
Lời giải:
a) Xét tam giác $ABC$ và $DEC$ có:
$\widehat{C}$ chung
$\widehat{BAC}=\widehat{EDC}=90^0$
$\Rightarrow \triangle ABC\sim \triangle DEC$ (g.g)
b) Xét tam giác $DEC$ và $DBF$ có:
$\widehat{EDC}=\widehat{BDF}=90^0$
$\widehat{DEC}=\widehat{DBF}(=90^0-\widehat{C})$
$\Rightarrow \triangle DEC\sim \triangle DBF$ (g.g)
$\Rightarrow \frac{DE}{DC}=\frac{DB}{DF}$
$\Rightarrow DE.DF=DB.DC$ (đpcm)
