Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(\widehat{A}=80^o;\widehat{B}=50^o\Rightarrow\widehat{C}=180^o-\widehat{A}-\widehat{B}=180^o-80^o-50^o=50^o\)
\(\Rightarrow\widehat{C}=\widehat{B}< \widehat{A}\)
\(a,\) Cạnh lớn nhất là cạnh BC, bé nhất là cạnh AC
\(b,\) Tam giác ABC là tam giác cân vì có \(\widehat{C}=\widehat{B}=45^o\)

`a,` vì Tam giác `ABC` có \(\widehat{A}=110^0\)
`=>` Tam giác `ABC` là tam giác tù.
`b,` Cạnh đối diện của \(\widehat{A}\) là cạnh `BC`
`=>` Cạnh lớn nhất của Tam giác `ABC` là cạnh `BC`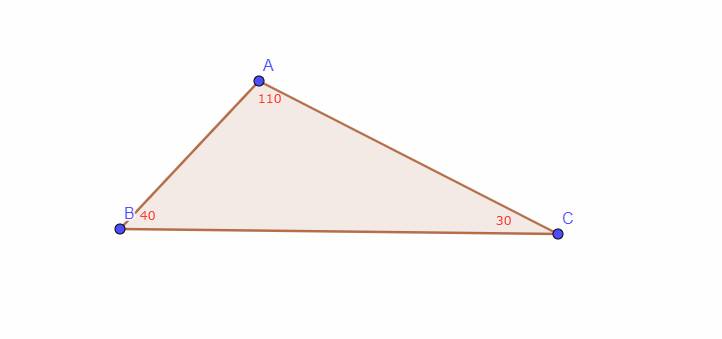

a: \(\widehat{B}=90^0\)
Xét ΔABC có \(\widehat{C}< \widehat{A}< \widehat{B}\)
nên AB<BC<AC
b: Xét ΔBAC có
BA<BC
mà AH là hình chiếu của BA trên AC
và CH là hình chiếu của BC trên AC
nên AH<CH

Ta có
\(AB=AC\\ \Rightarrow\Delta ABC.cân.tại.A\)
Xét \(\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\Delta\)ABC cân tại A nên:
\(\widehat{B}=\widehat{C}\\ \Rightarrow\widehat{B}=\dfrac{180^o-\widehat{A}}{2}=\dfrac{100}{2}=50^o\)
Do \(\Delta\)ABC cân nên AB = AC và không có cạnh lớn nhất

a: góc B=góc C=(180-45)/2=67,5 độ
Vì góc A<góc B=góc C
nên BC<AB=AC
b: XetΔAHB vuông tại H và ΔAHC vuông tai H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
c: ΔABC cân tại A
mà AH là đường cao
nên AH là trung trực của BC

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}+60^0=90^0\)
hay \(\widehat{ACB}=30^0\)(1)
Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\left(30^0< 60^0< 90^0\right)\)
nên AB<AC<BC
b) Xét ΔABD vuông tại A và ΔKBD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)(BD là tia phân giác của \(\widehat{ABK}\))
Do đó: ΔABD=ΔKBD(cạnh huyền-góc nhọn)
c) Ta có: BD là tia phân giác của \(\widehat{ABC}\)(gt)
nên \(\widehat{ABD}=\widehat{DBC}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{DBC}=\widehat{DCB}\)
Xét ΔDBC có \(\widehat{DBC}=\widehat{DCB}\)(cmt)
nên ΔDBC cân tại D(Định lí đảo của tam giác cân)
Xét ΔBDK vuông tại K và ΔCDK vuông tại K có
DB=DC(ΔDBC cân tại D)
DK chung
Do đó: ΔBDK=ΔCDK(Cạnh huyền-cạnh góc vuông)
Suy ra: BK=CK(hai cạnh tương ứng)
hay K là trung điểm của BC(Đpcm)
a) ta có: góc a + góc b + góc c = 180
hay 80 + 50 + góc c = 180
=> góc c = 180 - 80 - 50 = 50 độ
vì 80 độ > 50 độ => góc a là góc lớn nhất trong tam giác => cạnh lớn nhất là cạnh bc (vì cạnh đối diện với góc lớn hơn là cạnh lớn hơn)
b) \(\Delta ABC\) là tam giác cân vì có 2 góc ở đáy bằng nhau, đều bằng 50 độ
a, trong tam giác abc có góc a=80 độ,góc b= 50 độ
=>góc c =50 độ
=>góc a là góc lớn nhất
=>cạnh đối diện với góc a là bc
=>bc lớn nhất
b,vì góc b=50độ;góc c=50 độ
=>tam giác abc cân ở a