Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Kẻ KE,KD,KF lần lượt vuông góc AB,BC,AC
Xét ΔBEK vuông tại E và ΔBDK vuông tại D có
BK chung
góc EBK=góc DBK
=>ΔBEK=ΔBDK
=>KD=KE
Xet ΔCDK vuông tại D và ΔCFK vuông tại F có
CK chung
góc DCK=góc FCK
=>ΔCDK=ΔCFK
=>KD=KF=KE
=>K cách đều AB,AC
b: góc ABC+góc ACB=180-50=130 độ
góc EBC+góc FCB=360 độ-130 độ=260 độ
=>góc KBC+góc KCB=130 độ
=>góc BKC=50 độ

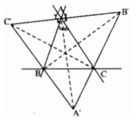
Ta có AA′⊥ AB′ vì chúng là hai tia phân giác của hai góc kề bù. Tương tự AA′⊥ AC′. Vì qua A chỉ có một đường vuông góc với AA' nên ba điểm B', A, C' thẳng hàng và AA′⊥ B′C′, hay A'A là một đường cao của tam giác A'B'C'. Hoàn toàn tương tự ta chứng minh được BB' và CC' là hai đường cao của tam giác A'B'C'.
Mặt khác theo cách chứng minh của bài 9.5 ta có AA', BB', CC' là ba tia phân giác của các góc A, B, C của tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.

ai kết bạn với mik nha
fan MTP
ai chơi truy kích kết ban lun nha

3)- theo bài tao có :A+B+C=180 độ.(định lí tổng ba góc của 1 tam giác)
C:B:A=1:3:6 => C/1=B/3=A/6=(A+B+C)/(1+3+6)=180/10=18
Do đó :C/1=18 B/3=18 A/6=18
=>C=18 độ =>B=54 độ =>A=104 độ