Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có AM/AB =AN/AC =3/5 .Suy ra theo talet ta có MN//BC
b) ta có MK // BI nên tam giác AMK đồng dạng tam giác ABI . Suy ra AM /AB =MK /BI => MK = BI . AM/AB
Tương tự tam giác AKN đd tam giác AIC nên suy ra AN/AC =KN /IC . Suy ra NK = IC .AN /AC
mÀ IB = IC & AM/AB =AN/AC nên suy ra MK =NK (ĐPCM )
Bạn kẻ hình giúp mình
a) ta có:
AMMB=32,ANNC=7,55=32⇒AMMB=ANNC(=32)AMMB=32,ANNC=7,55=32⇒AMMB=ANNC(=32)
⇒⇒ MN//BC( định lí talet đảo)
b) ta có K∈MN,I∈BC⇒NKK∈MN,I∈BC⇒NK//CI, KM//BI
⇒NKCI=AKAI,KMIB=AKAI⇒NKCI=KMIB(=AKAI)màCI=IB⇒NK=KM⇒NKCI=AKAI,KMIB=AKAI⇒NKCI=KMIB(=AKAI)màCI=IB⇒NK=KM
Vậy K là trung điểm NM

a) Ta có: \(\dfrac{AM}{MB}=\dfrac{3}{2}\)
\(\dfrac{AN}{NC}=\dfrac{7.5}{5}=\dfrac{3}{2}\)
Do đó: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)\(\left(=\dfrac{3}{2}\right)\)
Xét ΔABC có
M∈AB(gt)
N∈AC(gt)
\(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)(cmt)
Do đó: MN//BC(Định lí Ta lét đảo)
b) Xét ΔABI có
M∈AB(gt)
K∈AI(gt)
MK//BI(MN//BC, K∈MN, I∈BC)
Do đó: \(\dfrac{MK}{BI}=\dfrac{AK}{AI}\)(Hệ quả của Định lí Ta lét)(1)
Xét ΔACI có
K∈AI(gt)
N∈AC(gt)
KN//IC(MN//BC, K∈MN, I∈BC)
Do đó: \(\dfrac{KN}{IC}=\dfrac{AK}{AI}\)(Hệ quả của Định lí Ta lét)(2)
Từ (1) và (2) suy ra \(\dfrac{MK}{BI}=\dfrac{KN}{IC}\)
mà BI=IC(I là trung điểm của BC)
nên MK=KN
mà M,K,N thẳng hàng
nên K là trung điểm của MN(đpcm)

1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
=
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu củ
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQMa A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc A
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
QM
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
tóm lị là ABGHMN là sai

a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật

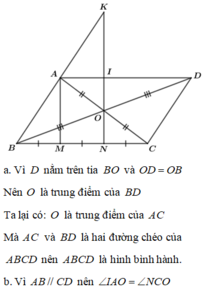

k đi mình làm cho
bạn giải dùm mình được hk