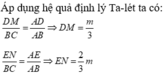Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

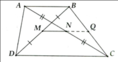
Ta có: \(DM//BC\)
Áp dụng định lí ta-let ta có:
\(\frac{DM}{BC}=\frac{AM}{AB}\Leftrightarrow\frac{DM}{6}=\frac{1}{3}\Leftrightarrow DM=2cm\)
Lại có: \(EN//BC\)
Áp dụng định lí ta-let ta có:
\(\frac{EN}{BC}=\frac{AN}{AB}\Leftrightarrow\frac{EN}{6}=\frac{2}{3}\Leftrightarrow EN=4cm\)
Vậy .......

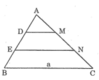
Trong ΔABC, ta có: DM // BC (gt)
Nên ![]() (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra : ![]() (3)
(3)
Từ (1) và (3) suy ra: 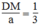
Suy ra: ![]()
Trong ΔABC, ta có: EN // BC (gt)
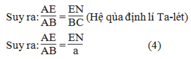
Từ (2) và (4) suy ra: 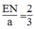 hay
hay 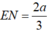

1: Xét ΔAEN có
D là trung điểm của AE
DM//EN
Do đó: M là trung điểm của AN
2: Xét hình thang BDMC có
E là trung điểm của BD
EN//BC//DM
Do đó: N là trung điểm của MC
Suy ra: NM=NC
mà NM=AM
nên AM=MN=NC
3: Xét hình thang DMCB có
E là trung điểm của BD
N là trung điểm của MC
Do đó: EN là đường trung bình của hình thang DMCB
Suy ra: \(EN=\dfrac{DM+BC}{2}\)
hay \(DM+BC=2\cdot EN\)