Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

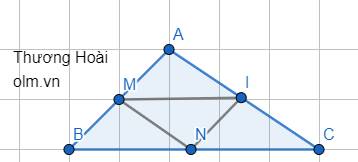
SBMN = \(\dfrac{1}{2}\)SABN ( hai tam giác có chung đường cao và tỉ số hai cạnh đáy tương ứng là \(\dfrac{1}{2}\))
SABN = \(\dfrac{1}{2}\) SABC ( hai tam giác có chung đường cao và tỉ số hai cạnh đáy là \(\dfrac{1}{2}\))
=> SBMN = \(\dfrac{1}{2}\times\dfrac{1}{2}\)SABC = \(\dfrac{1}{4}\) SABC
Chứng minh tương tự ta có :
SAMI = SCNI = \(\dfrac{1}{4}\) SABC
=> SMNI = Mặt khác ta có :
SABC = SBMN + SAMI + SCNI + SMNI
=> SMNI = SABC - SBMN - SAMI
=> SMNI = SABC - \(\dfrac{1}{4}\) SABC - \(\dfrac{1}{4}\) SABC - \(\dfrac{1}{4}\)SABC
=> SMNI = SABC \(\times\)( 1 - \(\dfrac{1}{4}\) - \(\dfrac{1}{4}\) - \(\dfrac{1}{4}\))
=> SMNI = \(\dfrac{1}{4}\)SABC

bn có thể tham khảo tại: https://olm.vn/hoi-dap/detail/96626463011.html

a) \(S_{ANB}=\dfrac{1}{2}\times S_{ABC}\) (chung đường cao hạ từ \(B\), \(AN=\dfrac{1}{2}\times AC\))
\(S_{AMC}=\dfrac{1}{2}\times S_{ABC}\) (chung đường cao hạ từ \(C\), \(AM=\dfrac{1}{2}\times AB\))
suy ra \(S_{AMC}=S_{ANB}\).
b) \(S_{MIB}=S_{ANB}-S_{AMIN},S_{NIC}=S_{AMC}-S_{AMIN}\)
mà \(S_{AMC}=S_{ANB}\) suy ra \(S_{MIB}=S_{NIC}\).