Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE
mà DE<DC
nên DB<DC
c: Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE

a: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
b: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
Do đó: ΔABE=ΔADE
Suy ra: EB=ED
c: Xét ΔBEG và ΔDEC có
BE=DE
\(\widehat{BEG}=\widehat{DEC}\)
EG=EC
Do đó: ΔBEG=ΔDEC
Suy ra: \(\widehat{EBG}=\widehat{EDC}\)
=>\(\widehat{EBG}+\widehat{ADE}=180^0\)
=>\(\widehat{EBG}+\widehat{EBA}=180^0\)
=>A,B,G thẳng hàng

a: Xét ΔAEB và ΔAEC có
AB=AC
góc BAE=góc CAE
AE chung
Do đó: ΔAEB=ΔAEC
b: Xét ΔEDB và ΔEDC có
ED chung
EB=EC
BD=CD
DO đó: ΔEDB=ΔEDC
=>góc BED=góc CED
=>ED là phân giác của góc BEC
c: Ta có: ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao

Hình tự vẽ nhá
Lời giải:
trên tia AB lấy điểm N sao cho AN=AC. Do AB>AC nên N nằm giữa A và B
Vậy AB - AC = AB - AN = BN
dễ dàng chứng minh đc tam giác AEN = tam giác AEC (cgc), suy ra EN = EC (2 cạnh tương ứng)
Xét tam giác EBN có: BN > EB - EN (hệ quả của bất đẳng thức trong tam giác)
mà BN = AB - AC ( đã chứng minh)
=> AB - AC > EB - EN
lại có EN = EC (đã chứng minh), suy ra AB - AC > EB - EC ( đpcm)
ko tránh khỏi thiếu sót, nếu sai ai đó sửa lại nhé. Thắc mắc gì cứ hỏi
_Hết_

Có gì sai sót mong bạn góp ý
Trên AC lấy điểm H sao cho AH=AB
Ta có:
AH=AC-CH
Mà AH=Ab
=>AB+AC-CH
=>CH=AC-AB(1)
Xét tam giác AHE và tam giác ABE có
AH=AB(gt)
HAE=BAE
AE chung
=> Tam giác AHE=tam giác ABE(c-g-c)
=>EH=EB(2 cạnh tương ứng)
Xét tam giác EHC có
HC>EC-EH
Mà EB=EH
=>HC>EC-EB(2)
Từ (1) và (2)=>AC-AB>EC-EB

1) xét tam giác ABE và tam giác ACE có:
AB=AC (GT)
\(\widehat{BAE}=\widehat{ACE}\)(GT)
AE cạnh chung
=> tam giác ABE= tam giác ACE
=>BE=EC

a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
Sửa đề: AB = BE (không phải AB = AE)
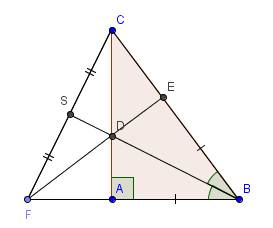
Gởi hình vẽ trước, đi công việc, tí sửa sau
Xét tam giác ABE và tam gi ác ACE có:
AB= AC (gt)
góc BAE=góc CAE( gt)
AE là cạnh chung
Suy ra: tam giác ABE = tam giác ACE ( c. g. c). (1)
=>EB= EC (2 cạnh tương ứng)
b, Xét tam giác ABD và tam giác ACD có:
AB=AC( gt)
góc BAD = góc CAD( gt)
AD là cạnh chung
Suy ra: tam giác ABD = tam giác ACD( c.g.c) (2)
Từ (1) và (2) => tam giác EBD= tam giác ECD
=> Góc BED = góc CED( 2 góc tương ứng)
Suy ra: ED là tia phân giác của BEC
Bạn tự ghi giả thiết, kết luận hen