Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác DFEC có
\(\widehat{DFC}=\widehat{DEC}\left(=90^0\right)\)
\(\widehat{DFC}\) và \(\widehat{DEC}\) là hai góc cùng nhìn cạnh DE
Do đó: DFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a:góc AHM+góc AKM=180 độ
=>AHMK nội tiếp
b: góc MBH+góc ABM=180 độ
góc MCK+góc ACM=180 độ
góc ABM=góc ACM
=>góc MBH=góc MCK
mà góc MHB=góc MKC
nên ΔMHB đồng dạng vơi ΔMKC
=>MH/MK=MB/MC
=>MH*MC=MK*MB

a: góc AHM+góc AKM=180 độ
=>AHMK là tứ giác nội tiếp
b: góc HBM=180 độ-góc ABM
góc KCM=180 độ-góc ACM
góc ABM=góc ACM
=>góc HBM=góc KCM
mà góc MHB=góc MKC
nên ΔMBH đồng dạng với ΔMCK
=>MB/MC=MH/MK
=>MB*MK=MC*MH

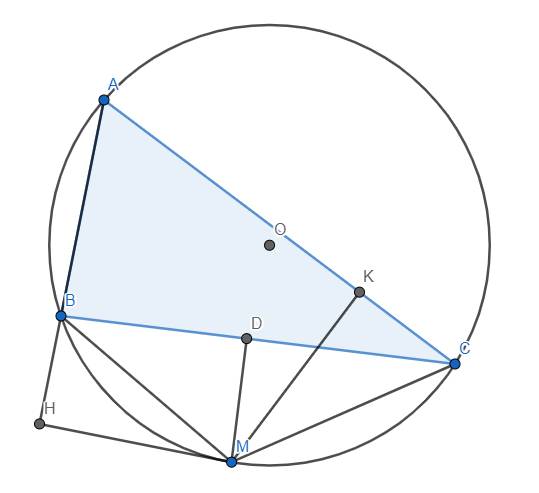
a) Theo đề bài, ta thấy \(\widehat{AHM}=\widehat{AKM}=90^o\) nên dễ dàng suy ra tứ giác AHMK nội tiếp do 2 góc đối bù nhau.
b) Do tứ giác AHMK nội tiếp nên \(\widehat{HMK}+\widehat{A}=180^o\). Tứ giác ABMC nội tiếp nên \(\widehat{BMC}+\widehat{A}=180^o\). Từ đó suy ra \(\widehat{HMK}=\widehat{BMC}\) hay \(\widehat{BMH}=\widehat{CMK}\). Lại có \(\widehat{MHB}=\widehat{MKC}=90^o\) nên \(\Delta MHB~\Delta MKC\left(g.g\right)\) \(\Rightarrow\dfrac{MH}{MK}=\dfrac{MB}{MC}\) \(\Rightarrowđpcm\)

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề