Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) * Vì tam giác ABC cân tại A nên đường cao đồng thời là đường trung tuyến ( t/c )
=> AM là đường trung tuyến ứng với cạnh BC
=> M là trung điểm của BC => MB = MC = 1/2 BC
b)-Vì tam giác ABC cân nên góc B = góc C
Vì MH vuông góc AB, MJ vuông góc AC nên \(\widehat{MHB}=90^o;\widehat{MKC}=90^o\)
Xét tam giác MHB và tam giác MKC có :
góc MHB = góc MKC ( =90 độ )
MB = MC ( cm ở câu a )
góc B = góc C (cmt )
Suy ra : \(\Delta MHB=\Delta MKC\) ( cạnh huyền - góc nhọn )
=> MH = MK ( cặp cạnh tương ứng )
* Gọi I là giao điểm của AM và HK
Vì tam giác MHB = tam giác MKC ( cmt )
=> BH = CK ( cặp canh t/ư)
Mà AB = AC ( tam giác ABC cân tại A )
=> AB - BH = AC - CK
=> AH = AK
=> Tam giác AHK cân tại A ( d/h )
Vì tam giác ABC cân tại A nên đường cao đồng thời là đường phân giác
=> AM là tia phân giác của góc BAC
Hay AI là tia phân giác của góc BAC
- Vì tam giác AHK cân nên phân giác đồng thời là đường cao, đường trung tuyến (t/c)
=> AI là đường cao đồng thời là trung tuyến của tam giác AHK
=> AM vuông góc HK tại I và I là trung điểm của HK
=> AM là đường trung trực của HK ( d/h )
c ) * Vì MH vuông góc AB tại H, E thuộc MH nên AM vuông góc AB tại H
Mà H là trung điểm EM
=> AB là đường trung trực EM
=> AE = AM ( t/c )
Tương tự : AC là đường trung trực của MF
=> AF = AM (t/c)
Suy ra : AE = AF ( = AM )
=> Tam giác AEF cân tại A ( d/h )

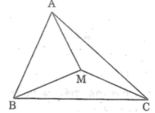
Trong ΔAMB, ta có:
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ΔAMC, ta có:
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ΔBMC, ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế (1), (2) và (3), ta có:
MA + MB + MA + MC + MB + MC > AB + AC + BC
⇔ 2(MA + MB + MC) > AB + AC + BC
Vậy MA + MB + MC > (AB + AC + BC) / 2

(h.45) Xét \(\Delta ABM:\)MA+MB>AB (1)
Xét \(\Delta AMC:\) MA+MC>AC (2)
Xét \(\Delta BMC:\) MB+MC>BC (3)
Cộng từng vế (1), (2), (3):
2(MA+MB+MC)>\(\text{AB+AC+BC}\)
Suy ra :
MA+MB+MC>\(\dfrac{\text{AB+AC+BC}}{2}\)