Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

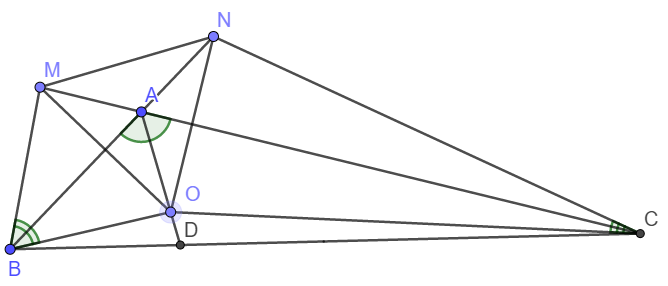
a) Xét tam giác ABC có ˆB+ˆC=60o⇒BAC=120oB^+C^=60o⇒BAC=120o
Do AD là phân giác nên ˆBAD=ˆCAD=60oBAD^=CAD^=60o
ˆMABMAB^ và ˆBACBAC^ là hai góc kề bù nên ˆMAB=180o−120o=60oMAB^=180o−120o=60o
Vậy thì ΔMAB=ΔOAB(g−c−g)ΔMAB=ΔOAB(g−c−g)
⇒AM=AO⇒AM=AO
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do ΔMAB=ΔOAB⇒AM=AO;BM=BOΔMAB=ΔOAB⇒AM=AO;BM=BO
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
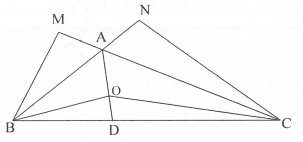 Ta có: △ABC có góc B+góc C=60 độ
Ta có: △ABC có góc B+góc C=60 độ
➩góc BAC =120 độ
ta có AD là phân giác
góc BAC=>BAD=CAD=\(\dfrac{1}{2}\)BAC=60 độ
△ABO và ΔABM có góc BAO= BAM=60 độ
AB chung
góc ABM =ABO
➩tam giác ABO =tam giác ABM (g.c.g)
➝AM=AO (*)
Ta chứng minh tương tự như trên:
tam giác ACO= tam giác ACN (g.c.g)
➝AN=AO(**)
Từ (*)(**) ⇒AM=AN (đpcm)


a) Xét tam giác ABC có \(\widehat{B}+\widehat{C}=60^o\Rightarrow BAC=120^o\)
Do AD là phân giác nên \(\widehat{BAD}=\widehat{CAD}=60^o\)
\(\widehat{MAB}\) và \(\widehat{BAC}\) là hai góc kề bù nên \(\widehat{MAB}=180^o-120^o=60^o\)
Vậy thì \(\Delta MAB=\Delta OAB\left(g-c-g\right)\)
\(\Rightarrow AM=AO\)
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do \(\Delta MAB=\Delta OAB\Rightarrow AM=AO;BM=BO\)
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath

a) Xét \(\Delta\)BAE và \(\Delta\)DAC có: ^BAE = ^DAC ( đối đỉnh ) ; AD = AB ( gt ) ; AE = AC ( gt )
=> \(\Delta\)BAE = \(\Delta\)DAC ( c.g.c)
=> BE = DC
b) Tương tự câu a dễ dàng cm đc: \(\Delta\)ADE = \(\Delta\)ABC => ^ADE = ^ABC => DE//BC
=> ^EDI = ^DIC mà ^EDI = ^BDI ( DI là phân giác ^BDE )
=> ^DIC = ^BDI hay ^DIB = ^IDB => \(\Delta\)BDI cân tại B.
c) Ta có: ^DBC là góc ngoài tại đỉnh B của \(\Delta\)BDI => ^DBC = ^BDI + ^BID = 2. ^BID = 2. ^CIF( theo b) (1)
Có: CF là phân giác ^BCA =>^BCF = ^ACF => ^BCA = ^BCF + ^ACF = 2. ^BCF = 2. ^ICF (2)
Lại có: ^CFD là góc ngoài của \(\Delta\)FCI => ^CFD = ^CIF + ^ICF (3)
Từ (1) ; (2) ; (3) => 2 .^CFD = 2 ^CIF + 2. ^ICF = ^DBC + ^BCA = ^DBC + ^CED ( ^CED = ^BCA vì ED //BC )

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath
bạn kham khảo tại link dưới đây nhé.
câu hỏi của Nguyễn Hoàng Giang - Toán lớp 7 - Học toán với OnlineMath