Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: DH=DE
DE<DC
=>DH<DC
c: Xét ΔAKC có
CH,KE là đường cao
CH căt KE tại D
=>D là trực tâm
=>AD vuông góc KC

`a,`
Xét `2 \Delta` vuông `AHD` và ` AED`:
\(\text{AD chung}\)
\(\text{AH = AE (gt)}\)
`=> \Delta AHD = \Delta AED (ch-cgv)`
`b,`
Vì `\Delta AHD = \Delta AED (a)`
`->`\(\text{DH = DE (2 cạnh tương ứng) (1)}\)
\(\text{Xét }\Delta\text{DEC :}\)
\(\widehat{\text{DEC}}=90^0\)
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`->`\(\text{DC là cạnh lớn nhất}\)
`->`\(\text{DC > DE (2)}\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
`->`\(\text{DC > DH.}\)
`c,` cho mình bỏ câu này;-;;; xin lỗi cậu nhiều;-;.
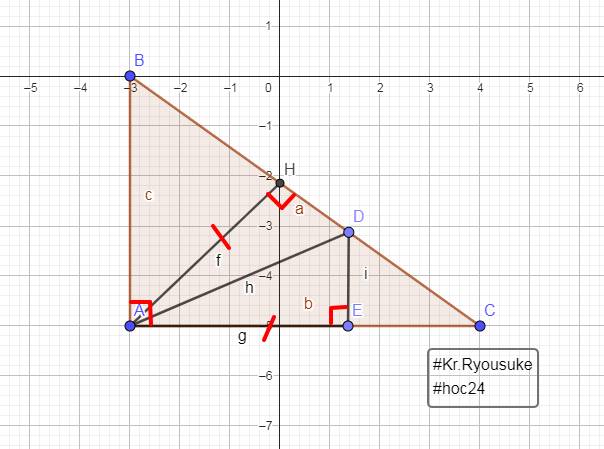

Xet ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
=>BC=DE
