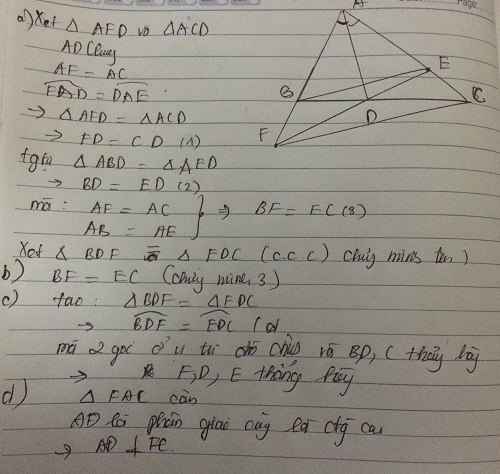Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED

a) Xét tam giác ABD và tam giác AED có:
AB=AE (GT)
góc BAD = góc EAD (AD là tia phân giác)
AD chung
Suy ra tam giác ABD=tam giác AED(CGC)
Suy ra BD=BE (hai cạnh tương ứng)
Xét tam giác AFD và tam giác ACD có:
AF=AC(GT)
Góc FAD= góc CAD (AD là tia phân giác của góc A)
AD chung
suy ra tam giác AFD và tam giác ACD(CGC)
suy ra DF=DC(2 cạnh tương ứng)
vì AB+BF=AE+EC (AF=AC)
Mà AB=AE(GT)
Suy ra BF=EC
Xet tam giác BFD và tam giác ECD có:
DB=DE(CMT)
DF=DC(CMT)
BF=EC(CMT)
Suy ra tam giac BFD=tamgiác ECD (CCC)
b) BF=EC (CMT)
c) vì tam giác BFD=tam giác ECD (CMT)
Suy ra gócBDF= gócEDC(2 GÓC TƯƠNG ỨNG)
Mà 2 góc này ở vị trí đối đỉnh
suy ra 3 điểm F,D,E thẳng hàng
d) xét tam giác AFD có:
AF=EC(GT)
Suy ra tam giác AFC cân tại A
mà AD là tia phân giac của góc A(gt)
suy ra AD cũng là đường cao của tam giác FAC
hay AD vuông góc FC

a+b) Xét \(\Delta AFE\) và \(\Delta ACB:\)
Ta có:\(A\) là góc chung
AE=AB (gt)
AF=AC (gt)
Vậy \(\Delta AFE=\Delta ACB\)(c.g.c)
Vậy \(AFE=ACB\) góc tương ứng 1
Xét \(\Delta ABD\) và \(\Delta AED\)
Ta có : \(BAD=EAD\) ( gt )
AD là cạnh chung
AB=AE (cạnh tương ứng)
Vậy \(\Delta ABD=\Delta AED\) ( c.g.c)
Vậy BD=ED (cạnh tương ứng ) (2)
Xét \(\Delta BDF\) và \(\Delta EDC\)
Ta có: EC=BF ( Do EA=BA và AC=AF mà EC=AC-EA, BF=AF-AB )
Từ (1)(2)
Vậy \(\Delta BDF=\Delta EDC\) ( c.g.c)
c. Ta có: \(BDF=EDC\) ( góc đối, cm câu a)
Nên F, D, E thẳng hàng
d. AC=AF (cạnh tương ứng, cm trên)
Nên AD là đường phân giác đồng thời đường cao ứng \(\Delta ACF\) cân nên AD vuông góc FC

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC