Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B → = 3 ; 12 , A C → = 4 ; − 1 ⇒ ( A B ) ⃗ . ( A C ) ⃗ = 3 . 4 + 12 . ( - 1 ) = 0 ⇒ ∆ A B C vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B

Ta có:
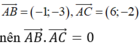
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.

Gọi I(a; b) là tâm đường tròn ngoại tiếp tam giác ABC.
A I 2 = B I 2 A I 2 = C I 2 ⇔ a − 0 2 + b − 2 2 = a + 2 2 + b − 8 2 a − 0 2 + b − 2 2 = a + 3 2 + b − 1 2
⇔ a 2 + b 2 − 4 b + 4 = a 2 + 4 a + 4 + b 2 − 16 b + 64 a 2 + b 2 − 4 b + 4 = a 2 + 6 a + 9 + b 2 − 2 b + 1
4 a − 12 b = − 64 6 a + 2 b = − 6 ⇔ a − 3 b = − 16 3 a + b = − 3
⇔ a = − 5 2 b = 9 2
Chọn B.

a: vecto AB=(1;1)
vecto AC=(2;6)
vecto BC=(1;5)
b: \(AB=\sqrt{1^2+1^2}=\sqrt{2}\)
\(AC=\sqrt{2^2+6^2}=2\sqrt{10}\)
\(BC=\sqrt{1^2+5^2}=\sqrt{26}\)
=>\(C=\sqrt{2}+2\sqrt{10}+\sqrt{26}\)
c: Tọa độ trung điểm của AB là:
x=(1+2)/2=1,5 và y=(-1+0)/2=-0,5
Tọa độ trung điểm của AC là;
x=(1+3)/2=2 và y=(-1+5)/2=4/2=2
Tọa độ trung điểm của BC là:
x=(2+3)/2=2,5 và y=(0+5)/2=2,5
d: ABCD là hình bình hành
=>vecto AB=vecto DC
=>3-x=1 và 5-y=1
=>x=2 và y=4

Gọi C(x;y) \(\Rightarrow\left\{{}\begin{matrix}x_G=\dfrac{x+2}{3}\\y_G=\dfrac{y-6}{3}\end{matrix}\right.\) \(\Rightarrow3\left(\dfrac{x+2}{3}\right)-\dfrac{y-6}{3}+1=0\)
\(\Leftrightarrow3x-y+15=0\Rightarrow y=3x+15\Rightarrow C\left(x;3x+15\right)\)
\(S_{ABC}=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
\(\Leftrightarrow3=\dfrac{1}{2}\left|-2\left(3x+19\right)-2\left(x-2\right)\right|\)
\(\Rightarrow x=...\)

Do G là trọng tâm tam giác ABC nên tọa độ G:
x G = x A + x B + x C 3 = − 1 + 5 + 0 3 = 4 3 y G = y A + y B + y C 3 = 1 + ( − 3 ) + 2 3 = 0 ⇒ G 4 3 ; 0
Điểm G1 là điểm đối xứng của G qua trục Oy nên G 1 − 4 3 ; 0
Đáp án D
Gọi tọa độ điểm H(a;b)
Ta có: A H → = a + 1 ; b − 1 , B H → = a ; b − 2 , B C → = 1 ; − 1 , A C → 2 ; 0
Do H là trực tâm tam giác ABC nên:
A C → . B H → = 0 B C → . A H → = 0 ⇒ 2. a + 0. b − 2 = 0 1. a + 1 − 1. b − 1 = 0 ⇒ a = 0 b = 2
Vậy H (0; 2).
Chọn A