Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

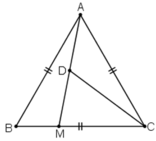
a) Do tam giác ABC là tam giác đều nên 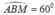 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
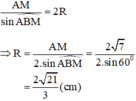
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
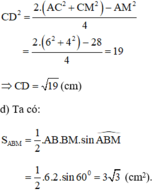

\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)

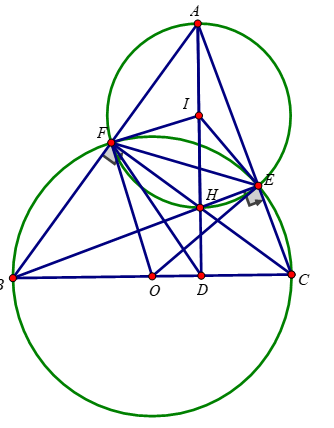
\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất

Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .
Ta có ADIE và BDCE là các tứ giác nội tiếp nên $\widehat{AID}=\widehat{AEI}=\widehat{ABC}$.
Suy ra BDIM nội tiếp.
Suy ra $AI.AM=AD.AB=AM^2-BM^2=3BM^2$ (vì AM=BC)
Suy ra $AI=\dfrac{3}{2}BM$ và $IM=AM-AI=\dfac{1}{2}BM$
Do đó $MI.MA=BM^2$, suy ra hai tam giác BIM và ABM đồng dạng theo c.g.c
Suy ra $\widehat{BIM}=\widehat{BAM}=\widehat{BCJ}$
Suy ra BI//CJ. Theo Talet thì $\dfrac{BI}{CJ}=\dfrac{BM}{CM}=1$.
Vậy $BICJ$ là hình bình hành.
Bài 11:Cho đường tròn(O) đường kính AB=2R. Điểm C thuộc đường tròn(C không trùng với A và B).Trên nửa mặt phẳng bờ AB có chứa điểm C kẻ tiếp tuyến à với (O).Gọi M là điểm chính giữa cung nhỏ AC. Tia BC cắt Ax tại Q,AM cắt BC tại N, AC cắt BM tại P.
a) Gọi K là điểm chính giữa cung AB(cung không chứa C).HỎi có thể xảy ra trường hợp 3 điểm Q,M,K thẳng hàng không?
b) Xác định vị trí của C trên nửa đường tròn tâm O để đường tròn ngoại tiếp tam giác MNQ tiếp xúc với (O).
Bài 12: Cho tứ giác ABCD có đường chéo BD không là phân giác của góc ABC và góc CDA.Một điểm P nằm trong tứ giác sao cho góc PBC=góc DBA; góc PDC = góc BDA.Chứng minh rằng tứ giác ABCD nội tiếp khi và chỉ khi AP=CP
Bài 13:Cho tam giác ABC có chu vi bằng 2p không đổi ngoại tiếp 1 đường tròn(O).Dựng tiếp tuyến MN với (O) sao cho MN song song với AC;M thuộc cạnh AB,N thuộc cạnh BC.Tính AC theo p để độ dài đoạn MN đạt giá trị lớn nhất.
Bài 14: Trong một tam giác cho trước hãy tìm bán kính lớn nhất của hai đường tròn bằng nhau tiếp xúc ngoài nhau đồng thời mỗi đường tròn tiếp xúc với hai cạnh của tam giác đó.
Bài 15: Trên cạnh AB của tam giác ABC lấy một điểm D sao cho đường tròn nột tiếp tam giác ACD và BCD bằng nhau
a) Tính đoạn CD theo các cạnh của tam giác
b)CMR: Điều kiện cần và đủ để góc C = 90 độ là điện tích tam giác ABC bằng diện tích hình vuông cạnh CD
Bài 16: Cho hình thang vuông ABCD có AB là cạnh đáy nhỏ,CD là cạnh đáy lớn,M là giao của AC và BD.Biết rằng hình thang ABCD ngoại tiếp đường tròn bán kính R.Tính diện tích tam giác ADM theo R
Bài 17:Cho tam giác ABC không cân,M là trung điểm cạnh BC,D là hình chiếu vuông góc của A trên BC; E và F tương ứng là các hình chiếu vuông góc của B và C trên đường kính đi qua A của đường tròn ngoại tiếp tam giác ABC.CMR: M là tâm đường tròn ngoại tiếp tam giác DEF
Bài 18: Cho đoạn thẳng AB, điểm C nằm giữa A và B, Tia Cx vuông góc với AB.Trên tia Cx lấy D và E sao cho CECB=CACD=3√CECB=CACD=3. Đường tròn ngoại tiếp tam giác ADC cắt đường tròn ngoại tiếp tam giác BEC tại H(H khác C). CMR: HC luôn đi qua một điểm cố định khi C chuyển động trên đoạn AB.Bài toán còn đúng không khi thay 3√3 bởi m cho trước(m>0)
Bài 19: Cho tam giác ABC nhọn và điểm M chuyện động trên đường thẳng BC.Vẽ trung trực của các đoạn BM và CM tương ứng cắt các đường thẳng AB và AC tại P và Q.CMR: Đường thẳng qua M và vuông góc với PQ đi qua 1 điểm cố định
Bài 20: Cho tam giác ABC và một đường tròn (O) đi qua A và C.Gọi K và N là các giao điểm của (O) với các cạnh AB,C.ĐƯờng tròn (O1) và (O2) ngoại tiếp tam giác ABC và tam giác KBN cắt nhau tại B và M.CMR: O1O2 song song với OM
hộ t 1 số bài tập với