Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Do ABC là tam giác cân tại A nên AB = AC hay AN = NB = CM = MA.
Xét tam giác AMB và ANC có:
AM = AN; AB = AC; góc A chung nên \(\Delta AMB=\Delta ANC\left(c-g-c\right)\)
b. Từ câu a, \(\widehat{ABM}=\widehat{ACN}\) (Hai góc tương ứng)
Mà tam giác ABC cân tại A nên \(\widehat{B}=\widehat{C}\)
Suy ra \(\widehat{DBC}=\widehat{DCB}\) hay tam giác BDC cân tại D.
c. Ta thấy \(\Delta ABE\) và \(\Delta ACE\) có : \(\widehat{B}=\widehat{C}=90^o;\) AB = AB; AE chung
nên \(\Delta ABE\)= \(\Delta ACE\left(ch-cgv\right)\Rightarrow EB=EC\)
Ta thấy AB = AC, DB = DC, EB = EC nên A, D, E cùng thuộc đường trung trực của BC. Vậy chúng thẳng hàng.

a) Xét \(\Delta ABC\)có : \(AB=AC\Rightarrow\Delta ABC\)cân
Có BM và CN là đường trung tuyến của tam giác \(\Rightarrow AM=AN=BN=CN\)
Xét \(\Delta AMB\)và \(\Delta ANC\)có : \(\hept{\begin{cases}AM=AN\left(cmt\right)\\\widehat{mAn}:chung\\AB=AC\left(gt\right)\end{cases}\Rightarrow\Delta AMB=\Delta ANC\left(c\cdot g\cdot c\right)}\)
b) Vì 2 đường trung tuyến BM và CN cắt nhau tại G => G là trọng tâm của \(\DeltaÂBC\)
=> AG là đường trung tuyến còn lại
mà \(\Delta ABC\)cân => AG vừa là đường trung tuyến và vừa là đường cao
\(\Rightarrow AG\perp BC\)hay \(AH\perp BC\)


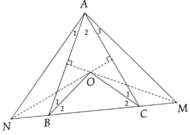
a: góc ABC=góc ACB=(180-50)/2=65 độ
b: Xét ΔAMB và ΔANC có
AM=AN
góc BAM chung
AB=AC
=>ΔAMB=ΔANC