Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cậu ghi rõ ràng hơn chút được không ạ . Cậu ghi AB AC ; BE BI mình không hiểu đc

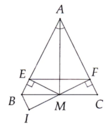
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{BAM}=\widehat{CAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
b) Xét \(\Delta AEM\left(\widehat{AEM}=90^o\right)\) và \(\Delta AFM\left(\widehat{AFM}=90^o\right)\) có:
\(\widehat{EAM}=\widehat{FAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta AEM=\Delta AFM\left(ch.gn\right)\)
\(\Rightarrow AE=AF\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta AEF\) cân tại \(A\)
c) Xét \(\Delta AEF\) cân tại \(A\) có \(AM\) là đường phân giác \(\widehat{A}\)
\(\Rightarrow AM\) cũng là đường trung trực \(\Delta AEF\)
\(\Rightarrow AM\perp EF\)
Tự vẽ hình
a, Tam giác AMB và tam giác AMC
AB = AC ( Tam giáC ABc cân )'
góc BAM = góc CAM ( AM là phân giác)
AM chung
=> Tam giác AMB = tam giác AMC ( c-g-c)
b, Xét tam giá AEM và tam giác AFM cs
góc AEM = góc AFM = 90 độ ( gt )
góc EAM = góc FAM ( AM là phân giác)
AM chung
=>tam giá AEM = tam giác AFM ( ch-gn)
=> AE = AF hay tam giác AEF cân tại A
c, Xét tam giác AEF cân tại A cs AM là tia phân giác đồng thời là đg cao
=> AM vuông góc vs EF

a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó:ΔAEM=ΔAFM
Suy ra:ME=MF
hay ΔMEF cân tại M
c: Ta có: AE=AF
ME=MF
Do đó: AM là đường trung trực của FE
hay AM⊥FE

a, Xét tam giác AMB và tam giác AMC có
AM _ chung
AB = AC
^MAB = ^MAC
Vậy tam giác AMB = tam giác AMC (c.g.c)
b, Xét tam giác AEM và tam giác AFM có
AM _ chung
^MAE = ^MAF
Vậy tam giác AEM = tam giác AFM (ch-gn)
=> AE = AF ( 2 cạnh tương ứng )
=> EM = FM ( 2 cạnh tương ứng )
Xét tam giác MEF có EM = FM
Vậy tam giác MEF cân tại M
c, AE/AB = AF/AC => EF // BC
mà tam giác ABC cân tại A có AM là phân giác
đồng thời là đường cao
=> AM vuông BC
=> AM vuông EF

a) Xét tam giác AMB và tam giác AMC ta có:
AM là cạnh chung
AB = AC (gt)
góc BAM = góc CAM ( AM là tia phân giác của góc BAC)
=> tam giác AMB = tam giác AMC ( c - g - c)
b) Xét tam giác AEM vuông tại E và tam giác AFM vuông tại F ta có:
AM là cạnh chung
góc EAM = góc FAM ( AM là tia p/g của góc BAC)
=> tam giác AEM = tam giác AFM ( ch - gn)
=> ME = MF ( 2 cạnh tương ứng)
c) Ta có:
BI // AC (gt)
IF _|_ AC tại F (gt)
=> FI _|_ BI tại I
Ta có:
góc EBM = góc FCM ( tam giác AMB = tam giác AMC)
góc IBM = góc FCM ( 2 góc so le trong và BI // AC)
=> góc EBM = góc IBM
Xét tam giác EBM vuông tại E và tam giác IBM vuông tại I ta có:
BM là cạnh chung
góc EBM = góc IBM (cmt)
=> tam giác EBM = tam giác IBM ( ch - gn)
=> BE = BI ( 2 cạnh tương ứng)
d) Ta có:
ME = MF ( tam giác AEM = tam giác ÀM)
ME = MB ( tam giác EBM = tam giác IBM)
=> MF = MB
=> M là trung điểm của BF ( M thuộc BF)
=> MB = 1/2 IF
Mà ME = MB ( cmt)
Nên ME = 1/2 IF ( đpcm)

tham khảo
a: Xét ΔAMB và ΔAMC có
AB=AC
ˆBAM=ˆCAMBAM^=CAM^
AM chug
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ˆEAM=ˆFAMEAM^=FAM^
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
c: Ta có: ΔAEM=ΔAFM
nên ME=MF
mà AE=AF
nên AM là đường trung trực của EF
hay AM⊥EF
a: Xét ΔAMB và ΔAMC có
AB=AC
ˆBAM=ˆCAMBAM^=CAM^
AM chug
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ˆEAM=ˆFAMEAM^=FAM^
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
c: Ta có: ΔAEM=ΔAFM
nên ME=MF
mà AE=AF
nên AM là đường trung trực của EF
hay AM⊥EF