Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) Ta có AM=MB và EM=MD ( đối xứng ) =>AEBD là hình bình hành
mà góc D = 90 (độ) => AEBD là hình chữ nhật
b) từ câu a =>AE//DC ; mà DC=DB (AD là đường cao của tam giác cân ABC =>là AD cũng đường trung tuyến)
=>ACDE là hình bình hành
c) để tứ giác AEBD là hình vuông thì:
như câu a thì AEBD là hình chữ nhật =>điều hiện là:AD=BD mà AD=BD =>tam giác ABC phải là tam giác vuông cân
d) S tam giác ABC= AD.BD/2 = AD.BD 1
S hình chữ nhật ABDE= AD.BD 2
Từ 1 và 2 =>S tam giác ABC = S hình chữ nhật ABDE (đpcm)

a/ Ta có MD là đường tb tam giác BAC nên ME//AC(1)
Mà vì \(\Delta AEM=\Delta BDM\left(c.g.c\right)\Rightarrow\widehat{AEM}=\widehat{BDM}\Rightarrow\)AE//BC(2)
Từ (1) và (2) suy ra ngay ĐPCM
b/ Từ giả thiết là D,E và A,B đối xứng với nhau qua điểm M suy ra AEBD là hbh
Từ đó để AEBD là hình chữ nhật thì MD phải vuông góc với BC Từ đó suy ra tam giác ACB phải vuông ở C

a. xét tam giác ABC, có:
M là trung điểm AB (giả thuyết)
D là trung điểm BC (AD là đường trung tuyến tam giác ABC)
=> MD là đường trung bình tam giác ABC
=> MD // AC
mà E thuộc MD (E là điểm đối xứng của D qua M)
=> DE // AC (1)
ta có: MD là đường trung bình tam giác ABC (chứng minh trên)
=> MD = \(\frac{1}{2}\)AC
mà M là trung điểm cua ED (E là điểm đối xứng của D qua M)
=> ED = AC (2)
từ (1),(2):
=> AEDC là hình bình hành (tứ giác có 1 cặp cạnh đối vừa song song, vừa bằng nhau) (chỗ này đề sai nên mình sửa lại là AEDC)
b. xét tứ giác AEBD, có:
M là trung điểm ED (E là điểm đối xúng của D qua M)
M là trung điểm AB (giả thuyết)
ED cắt AB tại M
=> AEBD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
xét tam giác ABC vuông A, có:
AD là đường trung tuyến (giả thuyết)
=> AD = BD
mà AEBD là hình bình hành (chứng minh trên)
=> AEBD là hình thoi (hình bình hành có 2 cặp cạnh kề bằng nhau)
C. ta có: D là trung điểm của BC (AD là đường trung tuyến)
=> BD = \(\frac{1}{2}\)BC
=> BD= \(\frac{5}{2}\)
=> BD= 2.5 cm
ta có: AEBD là hình thoi (chứng minh trên)
=> P(chu vi)AEBD = 2.5x4
= 10 cm

a) Xét tam giác ABC cân tại A: AD là phân giác (gt).
\(\Rightarrow\) AD là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) AD \(\perp\) BC.
Xét tứ giác AEBD có:
\(+\) I là trung điểm của AB (gt).
\(+\) I là trung điểm của ED (E là điểm đối xứng với D qua I).
\(\Rightarrow\) Tứ giác AEBD là hình bình hành (dhnb).
Mà \(\widehat{ADB}\) = 90o (AD \(\perp\) BC).
\(\Rightarrow\) Tứ giác AEBD là hình chữ nhật (dhnb).
b) Xét tam giác ABC cân tại A: AD là phân giác (gt).
\(\Rightarrow\) AD là trung tuyến (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) D là trung điểm của BC. \(\Rightarrow\) BD = DC.
Mà BD = EA (Tứ giác AEBD là hình chữ nhật).
\(\Rightarrow\) EA = DC (= BD).
Tứ giác AEBD là hình chữ nhật (cmt).
\(\Rightarrow\) EA // DC (Tính chất hình chữ nhật).
Xét tứ giác AEDC có:
\(+\) EA = DC (cmt).
\(+\) EA // DC (EA // BD).
\(\Rightarrow\) Tứ giác AEDC là hình bình hành (dhnb).

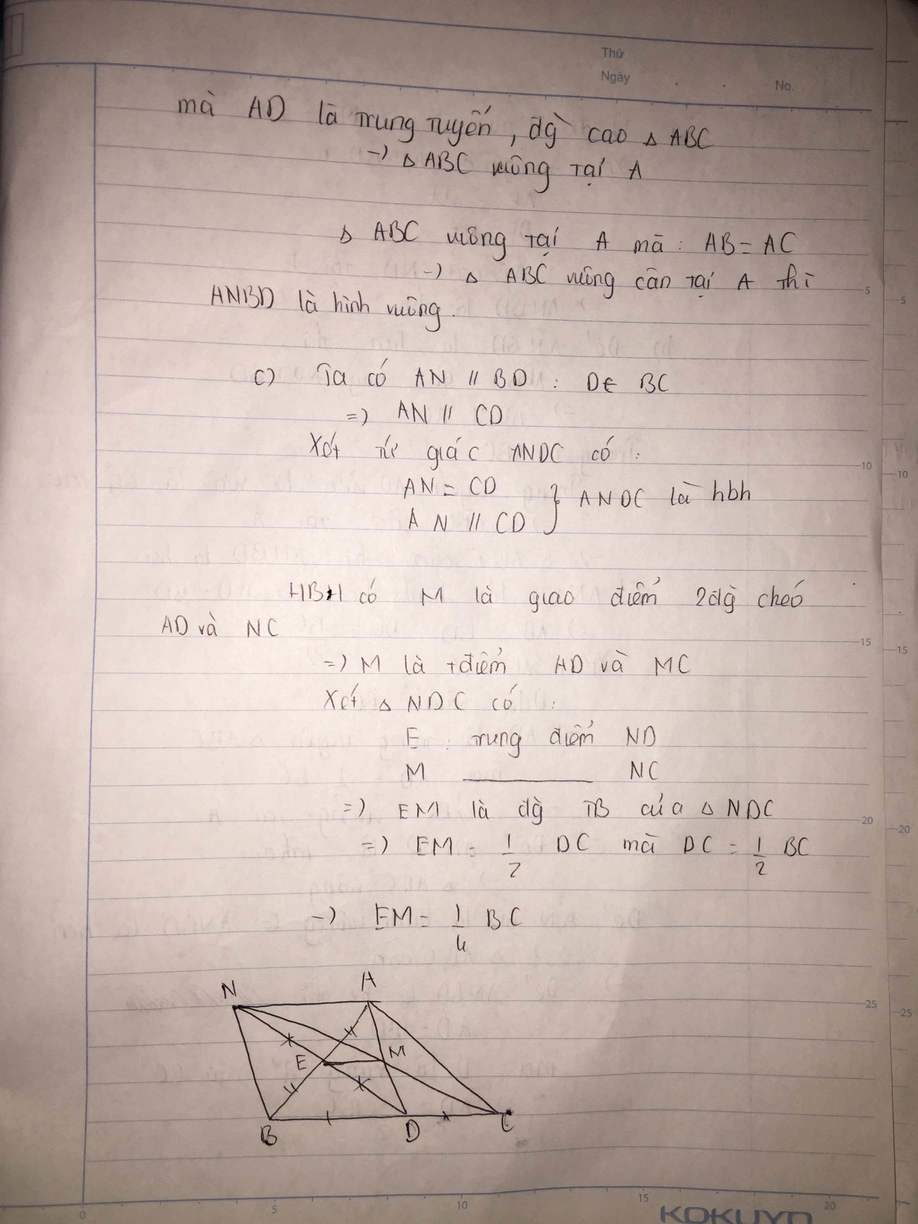
Bạn tự vẽ hình nhé.
a.
Xét tứ giác AEBD có:
AH = HB (H là trung điểm của AB)
HE = HD (vì E và D đối xứng với nhau qua H)
=> AEBD là hình bình hành.
Lại có: \(\widehat{ADB}=90^o\) (AD là đường trung tuyến của tam giác cân ABC)
Từ trên suy ra: AEBD là hình chữ nhật.
b.
Vì AEBD là hình chữ nhật nên ta có:
- AE // BD và AE = BD (1)
mà: BC // AE và BD = DC (2)
Từ (1), (2) suy ra: ACDE là hình bình hành.
c.
có: \(S_{AEBD}=AD.DB=\dfrac{1}{2}.AD.BC=S_{ABC}\)
d.
Để AEBD là hình vuông thì AD = BD
=> \(AD=\dfrac{1}{2}BC\) => Tg ABC vuông.
Mà AB = AC
=> Điều kiện của tam giác ABC là vuông cân tại A để AEBD là hình vuông.