Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
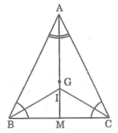
ΔABC cân tại A
⇒ phân giác AI đồng thời là trung tuyến
⇒ AI đi qua trọng tâm G của ΔABC
Vậy A, I, G thẳng hàng.
ban tic mjnh cai voi mjnh moi hoc lop 6 nhe xin loi chi nhieu lam
Kẻ đường phân giác của ˆAA^ và ˆCC^ cắt nhau tại I, AI cắt BC tại M.
∆ABC cân tại A.
Đường phân giác AM cũng là đường trung tuyến (tính chất tam giác cân)
G là trọng tâm của ∆ABC
⇒⇒ G ∈ AM
Vậy A, I, G thẳng hàng.
Bạn k cho mk nha !!!
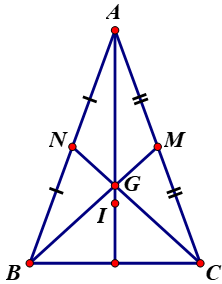
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà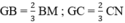 
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
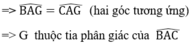
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của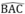 
Vì G, I cùng thuộc tia phân giác của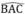 
nên A, G, I thẳng hàng
Giải
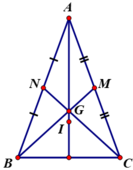
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà \(GB=\frac{2}{3}BM;GC=\frac{2}{3}CN\)(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\)( hai góc tương ứng )
\(\Rightarrow\)G là trọng tâm của \(\widehat{BAC}\)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc tia phân giác của \(\widehat{BAC}\)nên A, G, I thẳng hàng
