Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

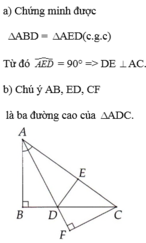
a) ΔABE = ΔDBE.
Xét hai tam giác vuông ABE và DBE có:
BA = BD (gt)
BE là cạnh chung
Do đó: ΔABE = ΔDBE (cạnh huyền - cạnh góc vuông)
b) BE là đường trung trực của AD.
Gọi giao điểm của AD và BE là I .
Vì ΔABE = ΔDBE (câu a) ⇒ ∠B1 = ∠B2 ( hai góc tương ứng)
Xét ΔABI và ΔDBI có:
BA = BD (gt)
∠B1 = ∠B2 (cmt)
BI : cạnh chung.
Do đó: ΔABI = ΔDBI (c - g - c)
⇒ AI = DI (hai cạnh tương ứng) (1)
∠I1 = ∠I2 (hai góc tương ứng) mà ∠I1 + ∠I2 = 180°
⇒ ∠I1 = ∠I2 = 180° : 2 = 90°
Hay BE ⊥ AD (2)
Từ (1) và (2) suy ra: BE là đường trung trực của AD
c) ΔBCF cân.
Vì ΔABE = ΔDBE (câu a) ⇒ AE = DE (hai cạnh tương ứng)
Xét hai tam giác vuông AEF và DEC có:
AE = DE (cmt)
∠E1 = ∠E2 (đối đỉnh)
Do đó: ΔAEF = ΔDEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = CD (hai cạnh tương ứng)
Ta có: BF = AB + AF và BC = BD + DC (3)
Mà: BA = BD (gt) và AF = DC (cmt) (4)
Từ (3) và (4) suy ra: BF = BC
Hay ΔBFC cân tại B.
d) B, E, H thẳng hàng.
Vì ∠B1 = ∠B2 (câu b)
Nên BE là phân giác của góc B (5)
Xét ΔFBH và ΔCBH có:
BF = BC (câu c)
FH = HC (trung điểm H của BC)
BH : chung
Do đó: ΔFBH = ΔCBH (c - c - c)
⇒ ∠FBH = ∠CBH (hai góc tương ứng)
⇒ BH là phân giác của góc B (6)
Từ (5) và (6) suy ra: B, E, H thẳng hàng.

Tham khảo tại link này nhé !
https://olm.vn/hoi-dap/detail/219404925266.html
a)Xét\(\Delta ABE\)và\(\Delta DBE\)có:
\(AB=DB\left(GT\right)\)
\(\widehat{BAE}=\widehat{BDE}\left(=90^o\right)\)
\(BE\)là cạnh chung
Do đó:\(\Delta ABE=\Delta DBE\)(cạnh huyền-cạnh gv)
b)Vì\(\Delta ABE=\Delta DBE\)(cm câu a) nên\(\widehat{ABE}=\widehat{DBE}\)(2 cạnh t/ứ)
Gọi\(K\)là giao điểm của\(AD\)và\(BE\)
Xét\(\Delta ABK\)và\(\Delta DBK\)có:
\(AB=DB\left(GT\right)\)
\(\widehat{ABK}=\widehat{DBK}\left(cmt\right)\)
\(BK\)là cạnh chung
Do đó:\(\Delta ABK=\Delta DBK\)(c-g-c)
\(\Rightarrow\widehat{AKB}=\widehat{DKB}\)(2 góc t/ứ)
\(AK=DK\)(2 cạnh t/ứ)
Ta có:\(\widehat{AKB}+\widehat{DKB}=180^o\)(2 góc KB)
mà\(\widehat{AKB}=\widehat{DKB}\left(cmt\right)\)
\(\Rightarrow\widehat{AKB}=\widehat{DKB}=\frac{180^o}{2}=90^o\)
\(\Rightarrow BK\perp AD\)
mà \(K\)là trung điểm của\(AD\)do\(AK=DK\left(cmt\right)\)
\(\Rightarrow BK\)là đường trung trực của\(AD\)
c)Xét\(\Delta ABC\)và\(\Delta DBF\)có:
\(\widehat{B}\)là góc chung
\(AB=DB\left(GT\right)\)
\(\widehat{BAC}=\widehat{BDF}\left(=90^o\right)\)
Do đó:\(\Delta ABC=\Delta DBF\)(g-c-g)
\(\Rightarrow BC=BF\)(2 cạnh t/ứ)
Xét\(\Delta BCF\)có:\(BC=BF\left(cmt\right)\)
Do đó:\(\Delta BCF\)cân tại\(A\)(Định nghĩa\(\Delta\)cân)
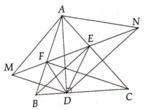


a: ΔABC can tại A
mà AD là trung tuyến
nên AD là phân giác
b: Xet ΔABE và ΔACF có
AB=AC
góc BAE chung
AE=AF
=>ΔABE=ΔACF
=>góc ABE=góc ACF=1/2*góc ABC
=>BE là phân giác của góc ABC
c: Xet ΔABC có
BE,CF,AD là phân giác
=>BE,CF,AD đồng quy