Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AH , BK cac duong cao
ke HF vuong goc AC=>HF//=BE/2=6
( tgBCE co HF duong trung binh)
tgiac AHC vuong tai H , duong cao HF
ta co 1/HF^2=1/AH^2+1/HC^2
=>HC=HF*AH/can(AH^2-HE^2)=6.5
=>BC=2HC=13
2)ta co b^2=a.b' ; c^2=a.c' vay b'/c'=(b/c)^2
do đó BD/CD=AB/AC(tinh chat duong pgiac)
vay BH/CH=(BD/CD)^2=BD^2/CD^2
ap dung tinh chat ty le thuc
BH/(CH+BH)=BD^2/(BD^2+CD^2)
BH/BC=BD^2/(BD^2+CD^2)
vi BH+CH=BC=>thay so vao BH=6.3
vay HD=BD-BH=1.2
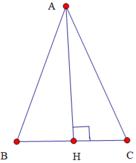
Kẻ AH vuông góc với BC, BK vuông góc với AC.
Tam giác ABC cân tại A nên AB = AC.
SABC = ½ AH . BC = ½ AH . 2BH (vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến.→ BH = CH)
SABC = ½ BK. AC
Do đó: ½ AH. 2BH = ½ BK. AC
→ AH . BH = ½ BK . AC
→ 15,6 . BH = ½ . 12. AB (AB = AC)
→ 15,6 . BH = 6. (AH + BH)
→ 15,6 / 6 .BH = 15,6 + BH
→ 2,6 BH = 15,6 + BH
→ 2,6 BH – BH = 15,6
→ 1,6 BH= 15,6
→ BH = 15,6 : 1,6
→ BH = 9,75
→ BC = 2. 9, 75 = 19,5

Làm trên này là fai có cáh giải nuk cháu ak, ghi kq chỉ tổ tốn côg

BẠn chỉ mình vẽ bán kính trên hoc24.vn đi rồi mình giải cho

Đáp án B
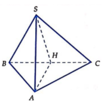
Gọi H là trung điểm B C ⇒ A H ⊥ B C → S B C ⊥ A B C A H ⊥ S H .
Xét hai tam giác vuông SHA và BHA có H A chung S A = B A = a ⇒ Δ S H A = Δ B H A .
⇒ S H = B H = C H ⇒ Δ S B C vuông tại S ⇒ R b = B H = B C 2 .
Dễ thấy
G T = B C ⇒ R = R b 2 + R d 2 − G T 2 4 = B H 2 + R d 2 − B C 2 4 = R d = a
Xét tam giác ABC, có:
sin C = A B 2 R = 1 2 ⇒ cos C = 3 2 ⇒ B C = 2 H C = 2 A C . cos C = a 3
Trong tam giác vuông SBC, ta có S C = B C 2 − S B 2 = a 2 .

Đáp án C
Gọi H là trung điểm B C ⇒ A H ⊥ B C ⇒ A H ⊥ S H
Ta có Δ S H A = Δ B H A , Δ S B C vuông tại S ⇒ R b = B H = B C 2
R = R b 2 + R d 2 − B C 2 4 = a
Xét Δ A B C có
sin C = A B 2 R = 1 2 ⇒ cos C = 3 2 ⇒ B C = 2 H C = a 3
Ta có trong tam giác vuông S B C : S C = B C 2 − S B 2 = a 2

Đáp án A
Chiều cao khối nón là A H = a 2 2 . Bán kính đáy là R = a 2 2
Thể tích khối nón là V = 1 3 π R 2 h = 1 3 π a 2 2 2 . a 2 2 = a 3 2 π 12

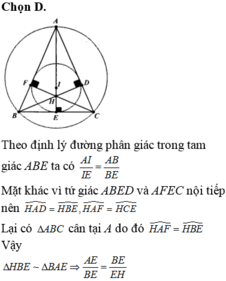

BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm