Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED = 4cm

a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

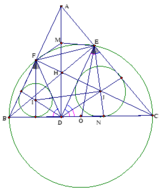
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
Tứ giác BFEC có B E C ^ = B F C ^ = 90 0
=> tứ giác BFEC nội tiếp đường tròn đường kính BC
Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF
∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^
∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)
=> ME=AH:2= MH do đó ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^
Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)
Nên O E B ^ + M E H ^ = 90 0 Suy ra M E O ^ = 90 0
⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^ = DFC ^
Tứ giác AFDC có A F C ^ = A D C ^ = 90 0 nên tứ giác AFDC nội tiếp đường tròn => B D F ^ = B A C ^
∆ BDF và ∆ BAC có B D F ^ = B A C ^ (cmt); B ^ chung do đó ∆ BDF ~ ∆ BAC(g-g)
Chứng minh tương tự ta có ∆ DEC ~ ∆ ABC(g-g)
Do đó ∆ DBF ~ ∆ DEC ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)
Vì ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác ⇒ D I D F = D J D C (2)
Từ (1) và (2) suy ra ∆ DIJ ~ ∆ DFC (c-g-c) => DIJ ^ = DFC ^

ta có
\(\widehat{AEH}=90^0;\widehat{AFH}=90^0\)
=> \(\widehat{AEH}+\widehat{AFH}=180^0\)
=> tứ giác AEHF nội tiếp được nhé
ta lại có AEB=ADB=90 độ
=> E , D cùng nhìn cạnh AB dưới 1 góc zuông
=> tứ giác AEDB nội tiếp được nha
b)ta có góc ACK = 90 độ ( góc nội tiếp chắn nửa đường tròn)
hai tam giác zuông ADB zà ACK có
ABD = AKC ( góc nội tiếp chắn cung AC )
=> tam giác ABD ~ tam giác AKC (g.g)
c) zẽ tiếp tuyến xy tại C của (O)
ta có OC \(\perp\) Cx (1)
=> góc ABC = góc DEC
mà góc ABC = góc ACx
nên góc ACx= góc DEC
do đó Cx//DE ( 2)
từ 1 zà 2 suy ra \(OC\perp DE\)
