Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)

tự kẻ hình :
a, có EI // AC (gt)
=> góc ACI = góc AIB (đồng vị)
có góc ACI = góc ABC do tam giác ABC cân tại A (gt)
=> góc EIB = góc EBI
=> tam giác EIB cân tại E (dh)
b, góc ACI = góc EIB (câu a)
góc ACI + góc FCO = 180
góc EIB + góc EIO = 180
=> góc FCO = góc EIO (1)
tam giác EIB cân tại E (câu a) => EI = EB (đn)
mà có EB = CF (gt)
=> FC = EI
xét tam giác COF và tam giác IOE có : góc CFO = góc OEI (so le trong CF // EI)
và (1)
=> tam giác COF = tam giác IOE (g-c-g)
=> FO = OE (đn)
tự kẻ hình :
a, có EI // AC (gt)
=> góc ACI = góc AIB (đồng vị)
có góc ACI = góc ABC do tam giác ABC cân tại A (gt)
=> góc EIB = góc EBI
=> tam giác EIB cân tại E (dh)
b, góc ACI = góc EIB (câu a)
góc ACI + góc FCO = 180
góc EIB + góc EIO = 180
=> góc FCO = góc EIO (1)
tam giác EIB cân tại E (câu a) => EI = EB (đn)
mà có EB = CF (gt)
=> FC = EI
xét tam giác COF và tam giác IOE có : góc CFO = góc OEI (so le trong CF // EI)
và (1)
=> tam giác COF = tam giác IOE (g-c-g)
=> FO = OE (đn)

`Answer:`

a. Theo giả thiết: EI//AF
`=>\hat{EIB}=\hat{ACB}=\hat{ABC}=\hat{EBI}` (Do `\triangleABC` cân ở `A`)
`=>\triangleEBI` cân ở `E`
`=>EB=EI`
b. Theo giải thiết: BE=CF=>EI=CF`
Xét `\triangleOEI` và `\triangleOCF:`
`EI=CF`
`\hat{OEI}=\hat{OFC}`
`\hat{OIE}=\hat{OCF}`
`=>\triangleOEI=\triangleOFC(g.c.g)`
`=>OE=OF`
c. Ta có: `KB⊥AB` và `KC⊥AC`
`=>KB^2=KA^2-AB^2=KA^2-AC^2=KC^2`
`=>KB=KC`
Mà `BE=CF`
`=>KE^2=KB^2+BE^2=KC^2+CF^2=KF^2`
`=>KE=KF`
`=>\triangleEKF` cân ở `K`
Mà theo phần b. `OE=OF=>O` là trung điểm `EF`
`=>OK⊥EF`

Ta có: DMB=MBC (so le trong)
mà DBM=MBC(giả thiết)
=>DMB=DBM.
=>DMB là tam giác cân(ĐPCM)
=>DM=DB*
Làm tương tự như trên ta có :
EMC=ECM.
=>MEC là tam giác cân.
=>EM=CE.**
Từ *và**,=>DB+CE=DM+ME=DE(ĐPCM).
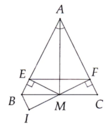
a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)