Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

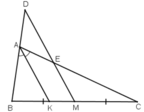
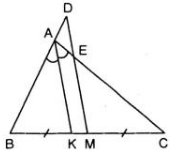
AK là đường phân giác của tam giác ABC nên:
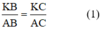
Ta có: MD // AK
⇒ ΔABK  ΔDBM và ΔECM
ΔDBM và ΔECM 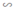 ΔACK
ΔACK
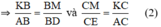
Từ (1) và (2) ta có: 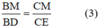
Do BM = CM (giả thiết) nên từ (3) suy ra: BD = CE.

Bài 1:
Xét tam giác $BDM$ có $AK\parallel DM$, áp dụng đl Talet:
$\frac{BA}{BD}=\frac{BK}{BM}=\frac{2BK}{BC}(*)$
Xét tam giác $CAK$ có $ME\parallel AK$, áp dụng đl Talet:
$\frac{CE}{CA}=\frac{CM}{CK}=\frac{BC}{2CK}(**)$
Lấy $(*)$ nhân $(**)$ thì:
$\frac{CE}{BD}.\frac{AB}{AC}=\frac{BK}{CK}$
Mà: $\frac{BK}{CK}=\frac{AB}{AC}$ (theo tính chất tia phân giác)
$\Rightarrow \frac{CE}{BD}=1$
$\Rightarrow CE=BD$ (đpcm)

a: Xét ΔBNQ có
C là trung điểm của BQ
CA//NQ
Do đó: A là trung điểm của NB
Xét ΔCPM có
B là trung điểm của CP
CA//MP
DO đó: A là trung điểm của CM
Xét tứ giác BMNC có
A là trung điểm chung của BN và MC
nên BMNC là hình bình hành
b: Để ANKM là hình bình hành
nên AM//KN và AN//KM
=>AB//MK và AB=MK
=>ABMK là hình bình hành
=>AI//BM
Xét ΔCBM có
A là trung điểm của CA
AI//BM
DO đó; I là trung điểm của BC

a) Xét tam giác AHD và tam giác CKD có:
AHD=CKD=90
\(D_1=D_2\) (2 góc đối đỉnh)
=> tam giác AHD đồng dạng tam giác CKD (g-g)
=> đpcm
b) Xét tam giác AHB và tam giác CKB có
AHB=BKC=90
ABD=DBC ( BD là tia phân giác ABC)
=> Tam giác AHB đồng dạng CKB (g-g)
=> \(\dfrac{AB}{HB}=\dfrac{BC}{KB}=>AB.KB=BC.HB\)