Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABC có góc B = 900, góc ACB = 300.
Suy ra góc A = 1800 - góc B - góc ACB = 180 - 90 - 30 = 600.
Mà AD là tia phân giác của góc A -> góc DAB=góc DAE = góc A / 2 = \(\frac{60^0}{2}=30^0\)
mà góc ABD bằng 900 -> góc ADB = 1800-900-300=600.
Vậy góc ADB bằng 600.
b) Xét hai tam giác BDA và tam giác EDA có :
AB = AE (GT)
góc BAD = góc EAD (cmt)
AD chung
Từ ba điều trên suy ra : tam giác BDA = tam giác EDA.
c) Ta có : góc DAE bằng = 300 (cmt)
mà góc ACB bằng 300 (GT)
Từ hai điều trên suy ra tam giác DAC cân tại D.
-> DA = DC (đpcm).

`a)`
Có `BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`
Xét `Delta ABD` và `DElta EBD` có :
`{:(BA=BE(GT),(hat(B_1)=hat(B_2)(cmt),(BD-chung):}}`
`=>Delta ABD=Delta EBD(c.g.c)(đpcm)`
`b)`
Có `Delta ABD=Delta EBD(cmt)=>hat(A)=hat(E_1)` ( 2 góc t/ứng )
mà `hat(A)=90^0`
nên `hat(E_1)=90^0(đpcm)`
`\color {blue} \text {_Namm_}`
`a,`
Xét Tam giác `ABD` và Tam giác `EBD` có:
`BA=BE (g``t)`
\(\widehat{ABD}=\widehat{EBD}\) `(` tia phân giác \(\widehat{ABE}\) `)`
`BD` chung
`=>` Tam giác `ABD =` Tam giác `EBD (c-g-c)`
`b,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`->`\(\widehat{BAD}=\widehat{BED}\) `(2` góc tương ứng `)`
Mà góc \(\widehat{A}\) vuông `(`\(\widehat{A}=90^0\) `)`
`-> `\(\widehat{BAD}=\widehat{BED}=90^0\)
`c,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> DE=DA (2` cạnh tương ứng `)`
Xét Tam giác `DEC:`
\(\widehat{DEC}=90^0\) `-> DC` là cạnh lớn nhất `-> DC>DE`
Mà `DE=DA -> DC>DA`
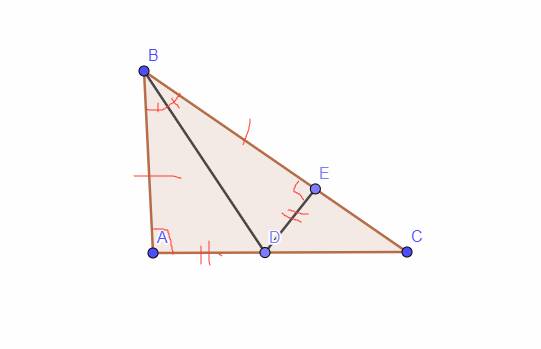

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=góc BAD=90 độ
=>DE vuông góc BC
c: DA=DE
mà DE<DC
nên DA<DC

a: Xét ΔADB và ΔADE có
AD chung
góc BAD=góc EAD
AB=AE
=>ΔADB=ΔADE
=>góc ABD=góc AED
b: Xét ΔAEF vuông tại A và ΔABC vuông tại A có
AE=AB
góc AEF=góc ABC
=>ΔAEF=ΔABC
=>AC=AF

Bài 2:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
=>ΔDAE cân tại D
c: ΔADB vuông tại A
=>AD<DB

a) Tam giác ABC có góc B = 900, góc ACB = 300.
Suy ra góc A = 1800 - góc B - góc ACB = 180 - 90 - 30 = 600.
Mà AD là tia phân giác của góc A -> góc DAB=góc DAE = góc A / 2 = 6002=3006002=300
mà góc ABD bằng 900 -> góc ADB = 1800-900-300=600.
Vậy góc ADB bằng 600.
b) Xét hai tam giác BDA và tam giác EDA có :
AB = AE (GT)
góc BAD = góc EAD (cmt)
AD chung
Từ ba điều trên suy ra : tam giác BDA = tam giác EDA.
c) Ta có : góc DAE bằng = 300 (cmt)
mà góc ACB bằng 300 (GT)
Từ hai điều trên suy ra tam giác DAC cân tại D.
-> DA = DC (đpcm).