
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


số chẵn có công thức: \(A=2n\)
bình phương: \(B=4n^2⋮2\)
Suy ra điều phải chứng minh :))

a) Gọi n chẵn là 2a
⇒ n2 = 2a . 2a = 4a2 ⋮ 2
⇒ n chẵn thì n2 chẵn

Ta có n2 = n.n
mà n2 chẵn => n.n chẵn
=> n.n ⋮2
=> có ít nhất 1 số chia hết cho 2
mà n = n => n ⋮2
=> n chẵn (đpcm)
Ta có n2 = n.n
mà n2 chẵn
=> n.n chẵn
=> n.n 2
=> có ít nhất 1 số chia hết cho 2
mà n = n => n 2 => n chẵn (đpcm)


Đáp án: C
A = {0; 2; 4; 6; 8; 10}; B = {0; 1; 2; 3; 4; 5; 6}; C = {4; 5; 6; 7; 8; 9; 10}.
B ∪ C = {n ∈ N: 0 ≤ n ≤ 10}; A ∩ (B ∪ C) = A.
A\B = {8; 10}; A\C = {0; 2}; B \ C = {0; 1; 2; 3}
(A \ B) ∪ (A \ C) ∪ (B \ C) = {0; 1; 2; 3; 8; 10}
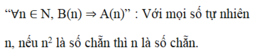
Giả sử n là số lẻ
Khi đó: n2 là số lẻ, trái với giả thiết
Vậy n là số chẵn.
Ta có n2 = n.n
mà n2 chẵn
=> n.n chẵn
=> n.n \(⋮\)2
=> có ít nhất 1 số chia hết cho 2
mà n = n => n \(⋮\)2 => n chẵn (đpcm)