Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo hệ thức Vi - ét, ta có: \(\left\{ \begin{array}{l} {x_1} + {x_2} = 2m + 1\\ {x_1}{x_2} = m - 7 \end{array} \right.\)
Theo đề bài, ta có: \({x_1} - {x_2} = 3\)
Từ đó ta có: \(\left\{ \begin{array}{l} {x_1} + {x_2} = 2m + 1\\ {x_1} - {x_2} = 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} {x_1} = m + 2\\ {x_2} = m - 1 \end{array} \right.\)
Với giá trị trên, ta có:
\(\begin{array}{l} \left( {m + 2} \right)\left( {m - 1} \right) = m - 7\\ \Leftrightarrow {m^2} + m - 2 = m - 7\\ \Leftrightarrow {m^2} = - 5 \end{array}\)
Vậy không có giá trị $m$ thỏa mãn
x2 - (2m + 1)x + m - 7 = 0
Có: \(\Delta\) = [-(2m + 1)]2 - 4.1.(m - 7) = 4m2 + 4m + 1 - 4m + 28 = 4m2 + 29 > 0
\(\Rightarrow\) x1 = \(\dfrac{2m+1+\sqrt{\Delta}}{2}\); x2 = \(\dfrac{2m+1-\sqrt{\Delta}}{2}\)
Lại có: x1 - x2 = 3
\(\Leftrightarrow\) \(\dfrac{2m+1+\sqrt{\Delta}-2m-1+\sqrt{\Delta}}{2}=3\)
\(\Leftrightarrow\) 2\(\sqrt{\Delta}\) = 6
\(\Leftrightarrow\) \(\sqrt{\Delta}\) = 3
\(\Leftrightarrow\) \(\Delta\) = 9
\(\Leftrightarrow\) 4m2 + 29 = 9
\(\Leftrightarrow\) m2 = -5 (Vô nghiệm)
Vậy không có giá trị m nào thỏa mãn đk
Chúc bn học tốt!

\(2x^2-\left(4m+3x\right)x+2m^2-1=0\)
\(-x^2-4mx+2m^2-1=0\)
\(\Delta=\left(4m\right)^2+4\left(2m^2-1\right)=24m^2-4\)
Để phương trình có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta>0\Leftrightarrow24m^2-4>0\Leftrightarrow m>\dfrac{1}{\sqrt{6}}\)
Vì phương trình có 2 nghiệm phân biệt, Áp dụng hệ thức Vi ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-4m\\x_1.x_2=1-2m^2\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=6\)
\(\Rightarrow\left(x_1+x_2\right)^2-2\left(x_1.x_2\right)=6\)
\(\Leftrightarrow16m^2-2\left(1-2m^2\right)=6\)
\(\Leftrightarrow20m^2=8\)
\(\Leftrightarrow m^2=\dfrac{2}{5}\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{\dfrac{2}{5}}\left(TM\right)\\m=-\sqrt{\dfrac{2}{5}}\left(\text{Loại vì m}>\dfrac{1}{\sqrt{6}}\right)\end{matrix}\right.\)
Vậy ...


\(-x^2+\left(m+2\right)x+2m=0\)
\(\Delta=\left(m+2\right)^2+8m=\left(m+6\right)^2-32\)
Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta>0\Leftrightarrow\left(m+2\right)^2>32\Leftrightarrow m>\sqrt{32}-2\)
Vì phương trình có 2 nghiệm phân biệt
Áp dụng hệ thức vi ét
\(\Rightarrow x_1+x_2=m+2\)
=> \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1+4x_2=0\end{matrix}\right.\)
\(\Rightarrow m=-3x_2-2\)
Bạn xem lại đề chứ k tìm được m luôn á

Để pt có 2 nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow m^2-4.1.\left(-2\right)>0\\ \Rightarrow m^2+8>0\left(luôn.đúng\right)\)
Vậy pt luôn có 2 nghiệm phân biệt
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=-2\end{matrix}\right.\)
\(x^2_1x_2+x_1x^2_2=2021\\ \Leftrightarrow x_1x_2\left(x_1+x_2\right)=2021\\ \Leftrightarrow\left(-m\right)\left(-2\right)=2021\\ \Leftrightarrow2m=2021\\ \Leftrightarrow m=\dfrac{2021}{2}\)
Để pt có 2 nghiệm thì
\(\Delta>0\\ \Rightarrow m^2-4.1.\left(-2\right)>0\\ \Rightarrow m^2+8>0.đúng.\forall.m\)
Vậy pt luôn có 2 nghiệm phân biệt
Áp dụng đlí Viét ta có
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=-m\\x_1x_2=\dfrac{c}{a}=-2\end{matrix}\right.\)
Lại có
\(x_1x_2+x_1x_2=2021\\ \Rightarrow x_1x_2\left(x_1+x_2\right)< 2021\\ \Rightarrow-2\left(-m\right)=2021\Rightarrow2m=2021\\ \Rightarrow m=\dfrac{2021}{2}\)

a: \(\Delta=\left(2m+2\right)^2-4\left(m^2-2m-3\right)\)
\(=4m^2+8m+4-4m^2+8m+12\)
=16m+16
Để phương trình luôn có nghiệm thì 16m+16>=0
hay m>=-1
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=28\)
\(\Leftrightarrow\left(2m+2\right)^2-3\left(m^2-2m-3\right)=28\)
\(\Leftrightarrow4m^2+8m+4-3m^2+6m+9=28\)
\(\Leftrightarrow m^2+14m-15=0\)
=>(m+15)(m-1)=0
=>m=1

Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(3-m^2\right)\)
\(=\left(2m-2\right)^2-4\left(3-m^2\right)\)
\(=4m^2-8m+4-12+4m^2\)
\(=8m^2-8m-8\)
\(=8\left(m^2-m-1\right)\)
Để phương trình có nghiệm thì \(\text{Δ}\ge0\)
\(\Leftrightarrow m^2-m-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge\dfrac{\sqrt{5}+1}{2}\\m\le\dfrac{-\sqrt{5}+1}{2}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1\cdot x_2=3-m^2\end{matrix}\right.\)
Ta có: \(x_1+x_2=3\)
\(\Leftrightarrow2m-2=3\)
\(\Leftrightarrow2m=5\)
hay \(m=\dfrac{5}{2}\)(thỏa ĐK)

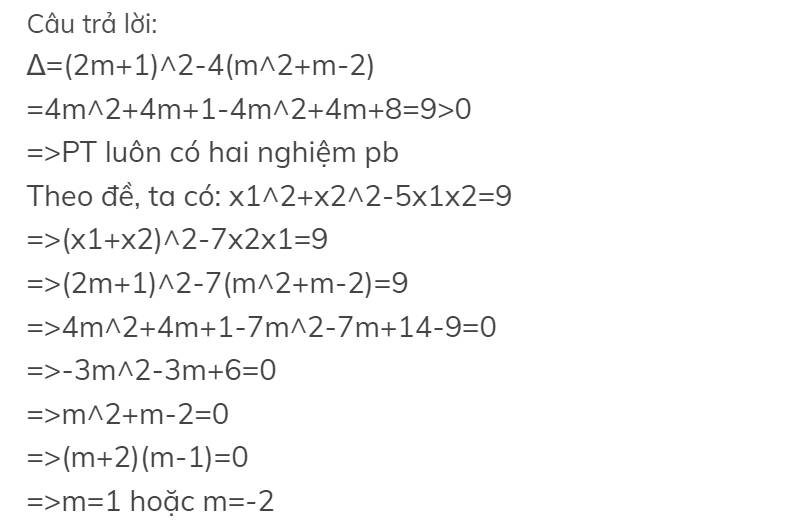
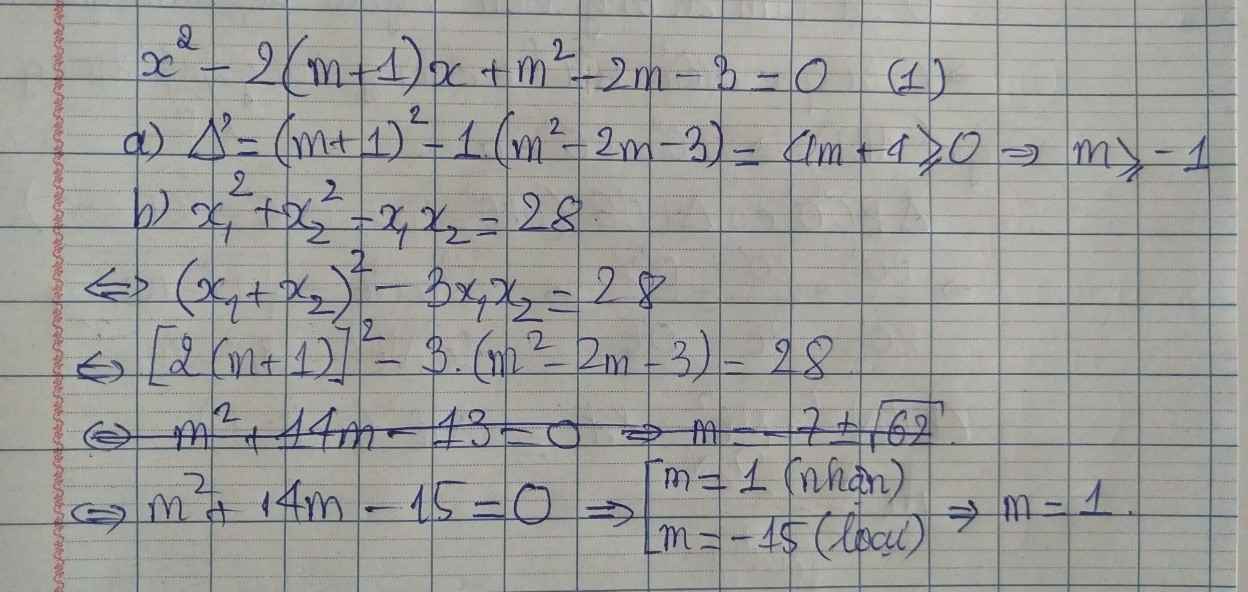
Δ=(-3)^2-4m^2=9-4m^2
Để phương trình có hai nghiệm thì 9-4m^2>=0
=>-2/3<=m<=2/3
x1^2-3x2+x1x2-m^2-2m-1>6-m^2
=>x1^2-x2(x1+x2)+x1x2>6-m^2+m^2+2m+1=2m+7
=>x1^2-x2^2>2m+7
=>(x1+x2)(x1-x2)>2m+7
=>(x1-x2)*3>2m+7
=>x1-x2>2/3m+7/3
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=3^2-4m^2=9-4m^2\)
=>\(x1-x2=\left|9-4m^2\right|\)
=>|9-4m^2|>2/3m+7/3
=>|4m^2-9|>2/3m+7/3
=>4m^2-9<-2/3m-7/3 hoặc 4m^2-9>2/3m+7/3
=>4m^2+2/3m-20/3<0 hoặc 4m^2-2/3m-34/3>0
=>\(\dfrac{-1-\sqrt{241}}{12}< m< \dfrac{-1+\sqrt{241}}{12}\) hoặc \(\left[{}\begin{matrix}m< \dfrac{1-\sqrt{409}}{12}\\m>\dfrac{1+\sqrt{409}}{12}\end{matrix}\right.\)
=>-2/3<=m<=2/3