Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
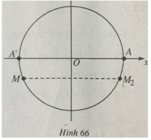
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
\(tan\left(\dfrac{3\pi}{2}-\alpha\right)+cot\left(3\pi-\alpha\right)-cos\left(\dfrac{\pi}{2}-\alpha\right)+2.sin\left(\pi+\alpha\right)\)
\(=tan\left(\pi+\dfrac{\pi}{2}-\alpha\right)+cot\left(-\alpha\right)-sin\alpha+2\left(sin\pi.cos\alpha+cos\pi.sin\alpha\right)\)
\(=tan\left(\dfrac{\pi}{2}-\alpha\right)-cot\alpha-sin\alpha+2.-sin\alpha\)
\(=cot\alpha-cot\alpha-3sin\alpha\)
\(=-3sin\alpha\)
Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.
Cách 1: Dựa vào mối quan hệ giữa các giá trị lượng giác của các cung có liên quan đặc biệt
a) sin (α – π) = - sin (π – α) (Áp dụng công thức sin (- α) = - sin α)
= -sin α (Áp dụng công thức sin (π – α) = sin α)
Mà sin α > 0 nên sin (α – π) < 0.
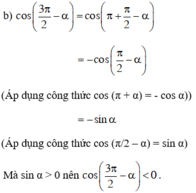
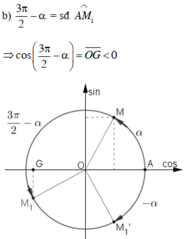
c) tan (α + π) = tan α.
Mà tan α > 0 nên tan (α + π) > 0.
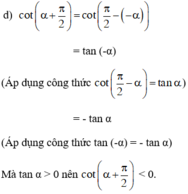
Cách 2: Dựa vào biểu diễn cung trên đường tròn lượng giác:
Vì 0 < α < π/2 nên ta biểu diễn α = sđ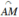 
như trên hình vẽ.
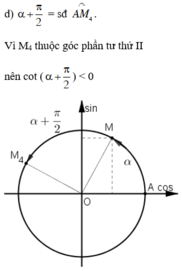
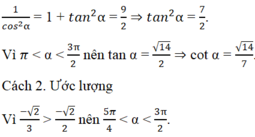
Suy ra 0 < cot α < 1. Vậy các phương án A, B, C bị loại.
Đáp án: D
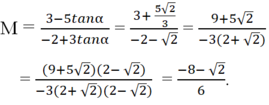
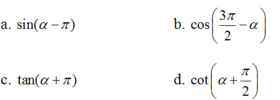
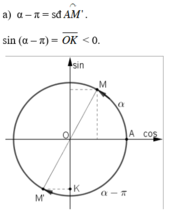
0 < 3π/2 - α < π/2 nên tan(3π/2 - α) > 0