Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chứng minh được OC là đường trung bình của hình thang AEFB nên C là trung điểm của EF. Chứng minh được AE=AH, BH=BF nên C H 2 = HA.HB = AE.BF
b, Ta có BE ∩ (O) = {H} => FE = AH ≤ AB
=> F E m a x = AB => C là điểm chính giữa AB

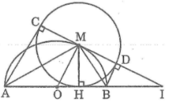
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi

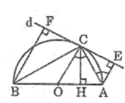
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90 °
Tam giác ABC vuông tại C có CH ⊥ AB
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
C H 2 = HA.HB (3)
Xét hai tam giác ACH và ACE, ta có:
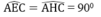
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : ∆ ACH = ∆ ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có:
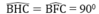
CH = CF (= CE)
BC chung
Suy ra: ∆ BCH = ∆ BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: C H 2 = AE.BF

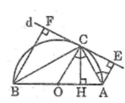
Ta có: AE // OC
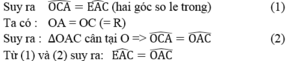
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE

Bài 1:
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

a, Ta có: E C A ^ + O C A ^ = 90 0 và A C H ^ + O A C ^ = 90 0
mà O A C ^ = O C A ^ (do tam giác AOC cân tại O)
Suy ra E C A ^ = A C H ^
Khi đó E A C ^ = H A C ^ (cùng lần lượt phụ với E C A ^ và A C H ^ ), ta có đpcm
b, Chứng minh tương tự suy ra BC là phân giác của F B H ^
Từ đó, chứng minh được BC vuông góc HF (1)
Tam giác ABC có trung tuyến OC = 1 2 AB. Suy ra tam giác ABC vuông tại C , tức là BC vuông góc với AC (2)
Từ (1),(2) suy ra đpcm
c, Ta có : AE+BF =2OC=2R không đổi
d, Ta có A E . B F ≤ A E + B F 2 4 = R 2
suy ra AE.BF lớn nhất = R 2 óAE=BF=R
Điều này xẩy ra khi C là điểm chính giữa cung AB