Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
ΔBMA nội tiếp đường tròn(B,M,A∈(O))
BA là đường kính(gt)
Do đó: ΔBMA vuông tại M(Định lí)
Xét (O) có
AB là đường kính của (O)(gt)
nên O là trung điểm của AB
Xét ΔBMA có
O là trung điểm của AB(gt)
C là trung điểm của AM(gt)
Do đó: OC là đường trung bình của ΔBMA(Định nghĩa đường trung bình của tam giác)
⇒OC//BM và \(OC=\dfrac{BM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: OC//BM(cmt)
BM⊥BA(ΔBMA vuông tại M)
Do đó: OC⊥AM(Định lí 2 từ vuông góc tới song song)
Xét tứ giác OCNB có
\(\widehat{OCN}\) và \(\widehat{OBN}\) là hai góc đối
\(\widehat{OCN}+\widehat{OBN}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OCNB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔNBA vuông tại B và ΔOCA vuông tại C có
\(\widehat{OAC}\) chung
Do đó: ΔNBA∼ΔOCA(g-g)
⇒\(\dfrac{AB}{AC}=\dfrac{AN}{AO}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AC\cdot AN=AO\cdot AB\)(đpcm)
c) Ta có: OC⊥AN(cmt)
mà E∈OC(gt)
nên EC⊥NA
Xét ΔNEA có
EC là đường cao ứng với cạnh NA(cmt)
AB là đường cao ứng với cạnh NE(gt)
EC cắt AB tại O(gt)
Do đó: O là trực tâm của ΔNEA(Định lí ba đường cao của tam giác)
⇒NO⊥AE(đpcm)

Gọi BE cắt đường tròn (O) tại điểm thứ hai là N. Gọi L là hình chiếu của I trên ME.
Dễ thấy ^BNA = 900. Suy ra \(\Delta\)BNA ~ \(\Delta\)BCE (g.g) => BN.BE = BC.BA
Cũng dễ có \(\Delta\)BMA ~ \(\Delta\)BCK (g.g) => BC.BA = BM.BK. Do đó BN.BE = BM.BK
Suy ra tứ giác KENM nội tiếp. Từ đây ta có biến đổi góc: ^KNA = 3600 - ^ANM - ^KNM
= (1800 - ^ANM) + (1800 - ^KNM) = ^ABM + (1800 - ^AEM) = ^EFM + ^MEF = ^KFA
=> 4 điểm A,K,N,F cùng thuộc một đường tròn. Nói cách khác, đường tròn (I) cắt (O) tại N khác A
=> OI vuông góc AN. Mà AN cũng vuông góc BE nên BE // OI (1)
Mặt khác dễ có E là trung điểm dây KF của (I) => IE vuông góc KF => IE // AB (2)
Từ (1);(2) suy ra BOIE là hình bình hành => IE = OB = const
Ta lại có EM,AB cố định => Góc hợp bởi EM và AB không đổi. Vì IE // AB nên ^IEL không đổi
=> Sin^IEL = const hay \(\frac{IL}{IE}=const\). Mà IE không đổi (cmt) nên IL cũng không đổi
Vậy I di động trên đường thẳng cố định song song với ME, cách ME một khoảng không đổi (đpcm).

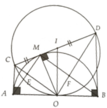
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.