Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a), b) HS tự chứng minh
c, AM = R 2 => S M O N S A P B = 25 16
d, V = 4 3 πR 3
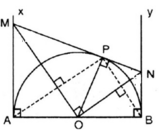
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc 
là góc nội tiếp chắn nửa đường tròn nên 
= 900
Tứ giác AOPM có:
Suy ra, tứ giác AOPM nội tiếp đường tròn.
Xét ∆ MON và ∆ APB có:
=> Hai tam giác MON và APB đồng dạng
b)
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
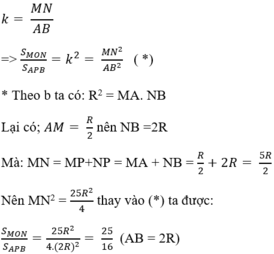
c) * Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
d) Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R.
nên thể tích khối cầu tạo ra là: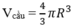 
Giải:
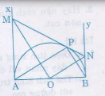
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3
Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R.
nên thể tích khối cầu tạo ra là: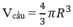 
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc 
là góc nội tiếp chắn nửa đường tròn nên 
= 900
Tứ giác AOPM có:
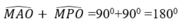
Suy ra, tứ giác AOPM nội tiếp đường tròn.
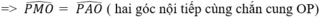
Xét ∆ MON và ∆ APB có:
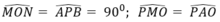
=> Hai tam giác MON và APB đồng dạng
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
c) Gọi giao điểm của BM với Ax là I. Từ M kẻ MK vuông góc với AB. BC cắt MK tại E.
Vì MK vuông góc AB => MK // AC // BD
EK // AC => \(\frac{EK}{AC}=\frac{BE}{BC}\); ME // IC => \(\frac{ME}{IC}=\frac{BE}{BC}\) => \(\frac{EK}{AC}=\frac{ME}{IC}\)
Tam giác MIA vuông tại M có CA = CM => góc CAM = góc CMA => góc CIM = góc CMI => tam giác CMI cân tại C => CI = CM => CM = CI = CA => EK = ME.
\(EK=ME\Rightarrow\frac{EK}{BD}=\frac{ME}{BD}\)mà \(\frac{ME}{BD}=\frac{CM}{CD}=\frac{AK}{AB}\Rightarrow\frac{EK}{BD}=\frac{AK}{AB}\)
=> Tam giác AKE đồng dạng với tam giác ABD (c.g.c) => góc EAK = góc DAK => A,E,D thẳng hàng => BC cắt AD tại E mà theo giả thiết BC cắt AD tại N => E trùng với N => H trùng với K => N là trung điểm MH.
* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
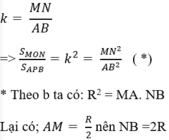
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
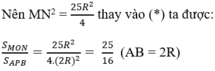
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)