Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

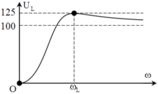
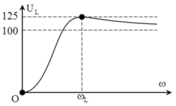
Từ đồ thị ta xác định được U = 100 U L m a x = U 1 − n − 2 = 125 ⇒ n = 3 , 6
Kết hợp với ω L ω C = ω R 2 n = ω L ω C ⇒ ω L = n ω R ≈ 190 π rad/s.
Đáp án A

Từ đồ thị ta xác định được U = 100 U L m a x = U 1 − n − 2 = 125 → n = 3,6
Kết hợp với ω L ω C = ω R 2 n = ω L ω C → ω L = n ω R ≈ 190 π rad/s.
Đáp án A

Đáp án: A
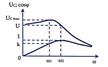
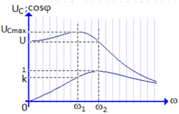
+ Khi ω = ω 2 ta thấy UC = U và cos φ = 1 => mạch đang xảy ra cộng hưởng:
UC = U → ZC2 = ZL2 = Z = R→ZC2.ZL2 = R2 →L/C = R2
+ Áp dụng công thức khi UCmax ta có:
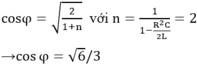

Chọn C.
Từ đề bài, ta thấy rằng ω 1 và 3 ω 1 là hai giá trị của tần số góc cho cùng cường độ dòng điện hiệu dụng trong mạch
![]()
Với ω 0 là giá trị tần số để mạch xảy ra cộng hưởng → Z L 0 = Z C 0 , ta chọn Z L 0 = Z C 0 = 1 , R = n.
Khi
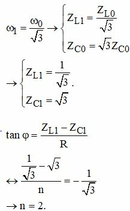
Tổng trở của mạch khi xảy ra cộng hưởng, ω = ω 1 là:
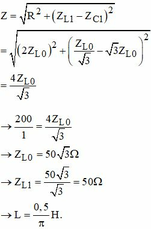

Đáp án C
+ Từ đề bài, ta thấy rằng ω 1 và 3 ω 1 là hai giá trị của tần số góc cho cùng cường độ dòng điện hiệu dụng trong mạch

+ Với ω 0 là giá trị của tần số để trong mạch xảy ra cộng hưởng → Z L 0 = Z C 0 , ta chọn Z L 0 = Z C 0 =1 , R = n .
+ Khi

Kết hợp với
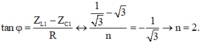
+ Tổng trở của mạch khi xảy ra cộng hưởng, ω = ω 1 là:


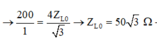


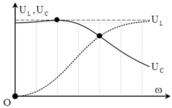
Từ đồ thị, ta thấy rằng ω R = 2 ω C → n = 4.
Áp dụng công thức chuẩn hóa .
U L m a x = U 1 − n − 2 ⇒ U L m a x U = 1 1 − n − 2 = 1 , 03
Đáp án C
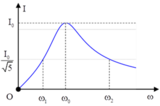

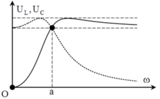
Với hai giá trị của tần số cho cùng dòng điện hiệu dụng trong mạch, ta luôn có : ω 1 ω 2 = 1 L C ⇒ Z L 1 = Z C 2
Từ hình vẽ ta có
U R 2 + Z L 2 − Z C 2 2 = U 5 R ⇔ R 2 + Z L 2 − Z C 2 ⏟ Z L 2 − Z L 1 2 = 5 R 2 (1)
Kết hợp với ω 2 − ω 1 = 400 π L = 3 π 4 ⇒ Z L 2 − Z L 1 = 300 Ω
Thay vào (1) ta tìm được : R = 150 Ω.
Đáp án D