Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: vecto AB=(1;1)
vecto AC=(2;6)
vecto BC=(1;5)
b: \(AB=\sqrt{1^2+1^2}=\sqrt{2}\)
\(AC=\sqrt{2^2+6^2}=2\sqrt{10}\)
\(BC=\sqrt{1^2+5^2}=\sqrt{26}\)
=>\(C=\sqrt{2}+2\sqrt{10}+\sqrt{26}\)
c: Tọa độ trung điểm của AB là:
x=(1+2)/2=1,5 và y=(-1+0)/2=-0,5
Tọa độ trung điểm của AC là;
x=(1+3)/2=2 và y=(-1+5)/2=4/2=2
Tọa độ trung điểm của BC là:
x=(2+3)/2=2,5 và y=(0+5)/2=2,5
d: ABCD là hình bình hành
=>vecto AB=vecto DC
=>3-x=1 và 5-y=1
=>x=2 và y=4

1/ M là TĐ của BC=> \(\left\{{}\begin{matrix}x_M=\frac{x_B+x_C}{2}\\y_M=\frac{y_B+y_C}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B+x_C=2\\y_B+y_C=-2\end{matrix}\right.\)
Tương tự \(\left\{{}\begin{matrix}x_C+x_A=6\\y_C+y_A=4\end{matrix}\right.;\left\{{}\begin{matrix}x_A+x_B=0\\y_A+y_B=-10\end{matrix}\right.\)
Tự kết hợp các hpt vs để tìm nhoa, bởi đến đây là siu ez rùi đoá :)
2/ \(\left\{{}\begin{matrix}x_G=\frac{x_A+x_B+x_C}{3}\\y_G=\frac{y_A+y_B+y_C}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2=\frac{1+x_B-2}{3}\\1=\frac{3+y_B+4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B=7\\y_B=-4\end{matrix}\right.\Rightarrow B\left(7;-4\right)\)
3/ \(\left\{{}\begin{matrix}x_C=\frac{x_A+x_B+x_D}{3}\\y_C=\frac{y_A+y_B+y_D}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2=\frac{-4+2+x_D}{3}\\-2=\frac{1+4+y_D}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=8\\y_D=-11\end{matrix}\right.\Rightarrow D\left(8;-11\right)\)

A’ là trung điểm của cạnh BC nên -4 = (xB+ xC)
=> xB+ xC = -8 (1)
Tương tự ta có xA+ xC = 4 (2)
xB+ xC = 4 (3)
=> xA+ xB+ xC =0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) và (2) ta có: xB= -4
(4) và (3) ta có: xC = -4
Tương tự ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG= = 0; yG =
= 1 => G(0,1).
xG’= ; yG’ =
= 1 => G'(0;1)
Rõ ràng G và G’ trùng nhau.

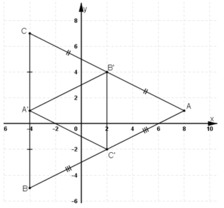
A’ là trung điểm của BC 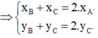
B’ là trung điểm của AC 
C’ là trung điểm của BA 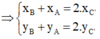
Gọi G là trọng tâm ΔABC và G’ là trọng tâm ΔA’B’C’
Ta có :
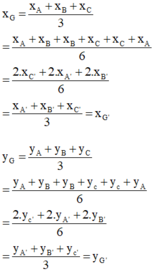
Vậy G ≡ G’ (đpcm)

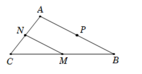
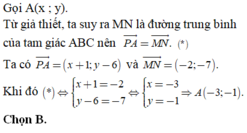
Tam giác ABC có M; N; P lần lượt là trung điểm của BC; AC ; AB nên PN và MN là đường trung bình của tam giác.
Suy ra: PN// BC và MN// AB.
Khi đó, tứ giác PNMB là hình bình hành.
Do đó, P B → = N M → với P B → ( x + 1 ; y − 3 ) ; N M → ( 0 ; − 2 )
⇒ x + 1 = 0 y − 3 = − 2 ⇔ x = − 1 y = 1 ⇒ B ( − 1 ; 1 )
Đáp án C