Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
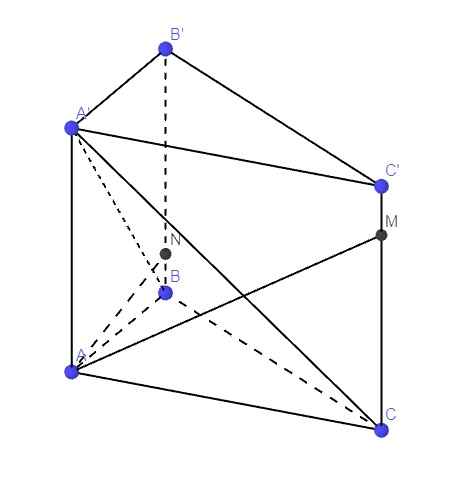
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)

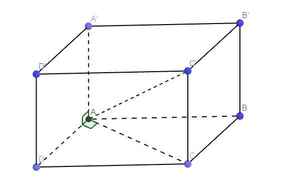
Do \(\left\{{}\begin{matrix}AA'\perp\left(ABCD\right)\Rightarrow AA'\perp AD\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(AA'C\right)\)
Mà \(AD||A'D'\Rightarrow A'D'\perp\left(AA'C\right)\)
Lại có \(AA'||CC'\Rightarrow C'\in\left(AA'C\right)\Rightarrow A'D'\perp AC'\) (1)
\(\left\{{}\begin{matrix}AA'\perp AC\\AA'=AC\end{matrix}\right.\) \(\Rightarrow\) tứ giác AA'C'C là hình vuông
\(\Rightarrow AC'\perp A'C\) (2)
(1);(2) \(\Rightarrow AC'\perp\left(A'D'C\right)\)

Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)

Chắc đề đúng là tính \(d\left(A;\left(BCC'B'\right)\right)\)
Gọi E là trung điểm BC \(\Rightarrow AE\perp BC\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AE\perp\left(BCC'B'\right)\)
\(\Rightarrow AE=d\left(A;\left(BCC'B'\right)\right)\)
Ta có: \(AE=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(\Rightarrow d\left(A;\left(BCC'B'\right)\right)=\dfrac{a\sqrt{3}}{2}\)

Bạn tự vẽ hình nha
a) Ta có :
A,P,N,M đồng phẳng
PN \(\in\) CC'D'D
AM\(\in\) AA'B'B
CC'D'D // AA'B'B
\(\Rightarrow\) PN // AM
\(\Rightarrow\) APNM là hình thang.
b)Gọi O là giao điểm của AC và BD.
\(\Delta ODC\infty\Delta OBA\)
\(\Rightarrow\frac{OC}{OA}=\frac{DC}{AB}=\frac{1}{2}\)
\(\Rightarrow\frac{AO}{AC}=\frac{2}{3}\)
Gọi I là giao điểm của AN và PM
\(\Delta\) ANC có OI // NC
\(\Rightarrow\frac{AI}{IN}=\frac{AO}{OC}=2\)
\(\Delta IPN\infty\Delta IMA\) ( AM // PN)
\(\Rightarrow\frac{AI}{IN}=\frac{AM}{NP}=2\)
cho hỏi tại sao OI song song NC ạ ?