Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là: | D. Hình vuông. |
A. 4cm. B. 7cm. C. 14cm. Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là: | D. 8cm. |
A. 10cm. B. 15cm. C. 5cm. | D. 8cm. |
Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. D. Hình vuông.
Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
A. 4cm. B. 7 cm. C. 14cm. D. 8cm.
Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:
A. 10cm. B. 15cm. C. 5cm. D. 8 cm

có bài tham khảo đây
1.Tứ giác ABCD có E,F,G,H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì, vì sao?
2.Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a)AI//CK
b)DM=MN=NB
3.Cho hình bình hành ABCD, E, F lần lượt là trung điểm các cạnh AB và CD. Gọi M, P, N lần lượt là giao điểm của AF và CE với BD
a)Chứng minh DM=MN=NP
b)Chứng minh tứ giác EMFN là hình bình hành
Gọi I và J lần lượt là trung điểm của BC và AD, Chứng minh 3 đường thẳng IJ, MN, EF đồng quy tại 1 điểm
Bài làm
Bài 1:
Kẻ đường chéo AC
có E,F,G,H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
suy ra EF là đường trung bình của tam giác ABC nên EF//=1/2AC (1)
GH là đường trung bình của tam giác ADC nên GH//=1/2AC (2)
Từ (1) và (2) suy ra EF//=GH nên EFGH là hình bình hành
Vì có hai cạnh đối song song và bằng nhau
Bài 2)
a) AK=1/2AB; CI=1/2CD
mà AB//=CD nên AK//=CI suy ra
AKCI là hình bình hành
do đó AI//CK
b) Xét tam giác CDN
có I là trung điểm CD mà IM//CN
nên M là trung điểm DN hay DM=MN (3)
(Theo định lý đường thẳng đi qua một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba)
Tương tự xét tam giác ABM cũng có BN=MN (4)
Từ (3) và (4) suy ra DM=MN=NB
Bài 3)
Câu a) làm ý như câu b) bài 2)
bâu b) chứng minh giống ý a bài 2 ta được AECF là hình bình hành
nên AF//CE => FM//EN (5)
Tam giác ABM=tam giác CDN (cgc) suy ra AM=CN
mà EN=1/2AM (t/c đường trung bình của tam giác)
FM=1/2 NC (t/c đường trung bình của tam giác)
do đó EN=MF (6)
từ (5) và (6) suy ra EMFN là hình bình hành.
câuc) I và J lần lượt là trung điểm của BC và AD
nên IJ đi qua trung điểm của EF (7)
MN và EF là hai đường chéo của hình bình hành ENFM nên MN đi qua trung điểm của EF (8)
Từ (7) và (8) suy ra 3 đường thẳng IJ, MN, EF đồng quy tại 1 điểm
Bạn hỏi dài quá. lần sau mỗi lần hỏi thì chỉ nên ghi 1 câu thôi, người trả lời đỡ ngại
và bạn nhanh chóng có được đáp án.
Chúc bạn học giỏi.
k mk nhé
Câu trả lời hay nhất: số các số có chữ số hàng chục trùng với chữ số hàng đơn vị : 9 số ( tương ứng với 9 chữ số 1, 2,...., 9 )
nếu chữ số hàng chục là x thì số các số có hàng chục là x và có số hàng đơn vị nhỏ hơn cũng là x ( vì số các số tự nhiên liều trước của 1 số, kể cả số 0 bằng chính số đó )
vậy nên số các số tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị là
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 ( số )
vậy có tất cả 45 tự nhiên có hai chữ số mà chữ số hàng chục lớn hơn chữ số hàng đơn vị

AE=BF=CG=DH
=>EB=FC=DG=HA
Xét ΔAEH vuông tại A và ΔBFE vuông tại B có
AE=BF
AH=BE
=>ΔAEH=ΔBFE
=>EH=EF
Xét ΔBEF vuông tại B và ΔCFG vuông tại C có
BE=CF
BF=CG
=>ΔBEF=ΔCFG
=>EF=FG
Xét ΔFCG vuông tại C và ΔGDH vuông tại D có
CF=DG
CG=DH
=>ΔFCG=ΔGDH
=>FG=GH
=>EF=FG=GH=HE
ΔAHE=ΔBEF
=>góc AEH=góc BFE
=>góc AEH+góc BEF=90 độ
=>góc HEF=90 độ
Xét tứ giác EHGF có
EH=HG=GF=EF
góc HEF=90 độ
=>EHGF là hình vuông

kẻ BD
ta có HA=HD
EA=EB
=> HE là đg tb cuả tam giác ABD
=> HE//BD; HE=1/2BD (1)
cmtt ta có GF là đg tb cuả tam giác CBD
=> GF//BD;GF=1/2BD (2)
Từ (1)và (2)
=>HE=GF(=1/2BD); HE//GF(//BD)
=> EFGH là hình bình hành

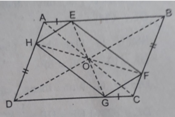
AE//CG, AE = CG nên AECG là hình bình hành ⇒ O là trung điểm của EG. Tương tự O là trung điểm của HF.

AE=BF=CG=DH
=>EB=FC=DG=HA
Xét ΔAEH vuông tại A và ΔBFE vuông tại B có
AE=BF
AH=BE
=>ΔAEH=ΔBFE
=>EH=EF
Xét ΔBEF vuông tại B và ΔCFG vuông tại C có
BE=CF
BF=CG
=>ΔBEF=ΔCFG
=>EF=FG
Xét ΔFCG vuông tại C và ΔGDH vuông tại D có
CF=DG
CG=DH
=>ΔFCG=ΔGDH
=>FG=GH
=>EF=FG=GH=HE
ΔAHE=ΔBEF
=>góc AEH=góc BFE
=>góc AEH+góc BEF=90 độ
=>góc HEF=90 độ
Xét tứ giác EHGF có
EH=HG=GF=EF
góc HEF=90 độ
=>EHGF là hình vuông
Chọn C