Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

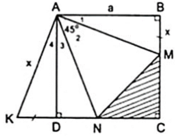
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
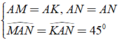 ⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.

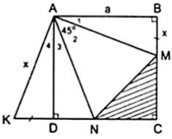
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
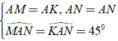 ⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.

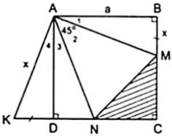
Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
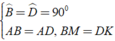
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
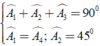
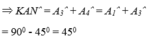

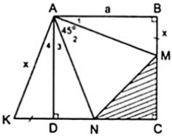
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
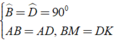
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
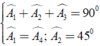
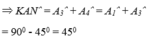

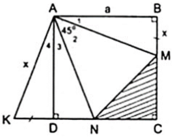
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
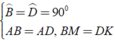
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
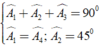
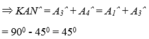

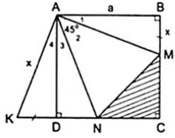
Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
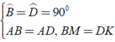 ⇒ Δ ABM = Δ ADK ( c - g - c )
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
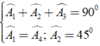
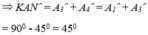

Xét hai tam giác vuông AKD và EAB có:
AD=AB
KD=EB
Do đó :tam giác AKD=TAM GIÁC EAB(2 cạnh góc vuông)
góc KAD= góc EAB
Mà góc DAF+EAB=45ĐỘ
SUY RA:KAF=45 ĐỘ
TAM GIÁC KAF= TAM GIÁC EAF(CGC)
SUY RA KF=FE ;GỌI a LÀ ĐỘ DÀI CẠNH HÌNH VUÔNG ABCD
CHU VI TAM GIÁC EFC LÀ:
EF+FC+CE
=KF+FC+EC
=KD+EC+DF+FC
=BE+EC+DE+EC=a+a=2a
a) Dễ chứng minh \(\Delta\)DKA = \(\Delta\)BMA.
Suy ra ^KAD = ^MAB. Mà ^MAB + ^MAN + ^NAD = 90o
Nên ^KAD + ^MAN + ^NAD = 90o hay ^KAD + ^NAD = 45o hay ^KAN = 45o
b)Chưa nghĩ ra