Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\Rightarrow OH\perp\left(ABCD\right)\)
\(\Rightarrow V_{O.ABCD}=\dfrac{1}{3}OH.S_{ABCD}\)
Đặt \(OH=x\Rightarrow BH=\sqrt{R^2-OH^2}=\sqrt{9a^2-x^2}\)
\(\Rightarrow AB=2BH=2\sqrt{9a^2-x^2}\)
\(\Rightarrow V=\dfrac{1}{3}x.3a.2\sqrt{9a^2-x^2}=a.2x.\sqrt{9a^2-x^2}\le a\left(x^2+9a^2-x^2\right)=9a^3\)
\(\Rightarrow V_{max}=9a^3\)

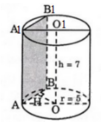
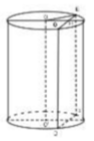
Mặt phẳng (P) song song với trục và cách trục 3cm, cắt hình trụ theo thiết diện là tứ giác A A 1 B 1 B .
Gọi H là trung điểm của AB.
Ta có 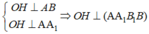

SAA1B1B = AB. AA1 = 8. 7 = 56 (cm2)
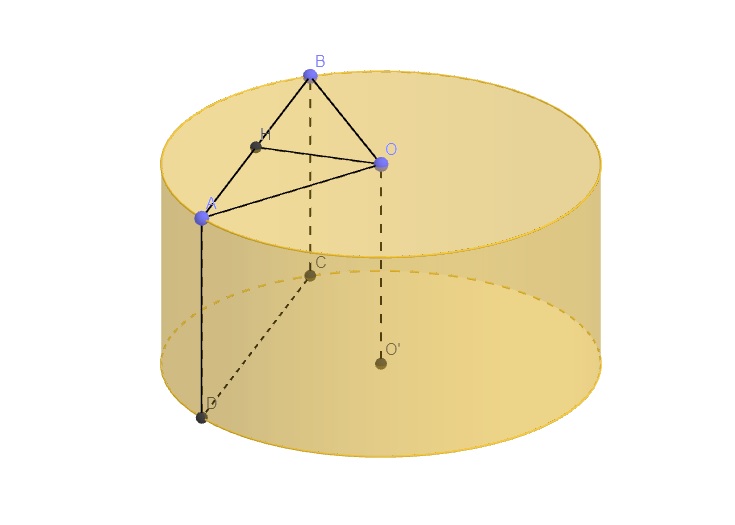
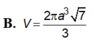

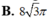

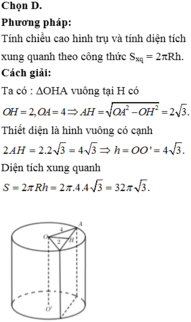

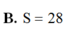

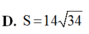

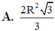
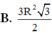

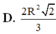

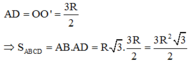

Hạ \(OH\perp AB\) tại H. Theo đề bài, ta thấy ngay \(\widehat{OAH}=30^o\). Lại có \(OA=\dfrac{OH}{\sin OAH}=\dfrac{\dfrac{10a}{3}}{\dfrac{1}{2}}=\dfrac{20a}{3}\)
Mặt khác, \(AH=OA.\cos OAH=\dfrac{20a}{3}.\dfrac{\sqrt{3}}{2}=\dfrac{10a\sqrt{3}}{3}\). Từ đó suy ra \(AB=2AH=2.\dfrac{10a\sqrt{3}}{3}=\dfrac{20a\sqrt{3}}{3}\)
Do ABCD là hình vuông nên \(AB=BC=\dfrac{20a\sqrt{3}}{3}\)
Vậy thể tích hình trụ đã cho là \(V_{trụ}=\pi.OA^2.BC=\pi.\left(\dfrac{20a}{3}\right)^2.\dfrac{20a\sqrt{3}}{3}\) \(=\dfrac{8000\sqrt{3}}{27}.\pi.a^3\) (đvdt)