Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

$#Shả$
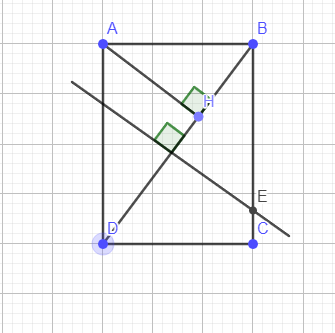
`a)` Xét `\triangleAHB` và `\triangleBCD` ta có `:`
`\hat{AHB}=\hat{BCD}=90^{o}`
`\hat{ABH}=\hat{BDC} ` (slt)
Vậy `\triangleAHB ` $\backsim$ `\triangleBCD` (g-g)
a) △AHB và △BCD có: \(\widehat{AHB}=\widehat{BCD}=90^0\); \(\widehat{ABH}=\widehat{BDC}\) (AB//DC).
\(\Rightarrow\)△AHB∼△BCD (g-g).
b) △ABD có: \(BD^2=AD^2+AB^2\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△AHB∼△BCD \(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}=\dfrac{HB}{CD}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{AB.BC}{BD}=\dfrac{3.4}{5}=2,4\left(cm\right)\\HB=\dfrac{AB.CD}{BD}=\dfrac{3.3}{5}=1,8\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.2,4.1,8=2,16\left(cm^2\right)\)
c) ABCD là hình chữ nhật, AC cắt BD tại O.
\(\Rightarrow\)O là trung điểm của AC và BD.
BD⊥DE tại D, CF⊥DE tại F. \(\Rightarrow\)BD//CF.
-△ODE có: IF//OD \(\Rightarrow\dfrac{IF}{OD}=\dfrac{EI}{EO}\).
-△OBE có: IC//OB \(\Rightarrow\dfrac{IC}{OB}=\dfrac{EI}{EO}=\dfrac{IF}{OD}\Rightarrow IC=IF\Rightarrow\)I là trung điểm CF.

a: Xét tứ giác BECF có
D là trung điểm chung của BC và EF
BE=EC
Do đó: BECF là hình thoi
b: Sửa đề: Tính diện tích BECF
\(BC=\sqrt{10^2-8^2}=6\left(cm\right)\)
DE=AB/2=4cm
=>EF=8cm
\(S_{BECF}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)

a: Xét tứ giác AKMI có
\(\widehat{AKM}=\widehat{AIM}=\widehat{KAI}=90^0\)
Do đó: AKMI là hình chữ nhật

A.
I là trung điểm của AB
I là trung điểm của MN (M đối xứng N qua I)
=> AMBN là hình bình hành
mà AM = MB (AM là đường trung tuyến của tam giác ABC vuông tại A)
=> AMBN là hình thoi
B.
Tam giác ABC vuông tại A có:
BC2 = AB2 + AC2 (định lý Pytago)
= 122 + 162
= 144 + 256
= 400 (cm)
BC = √400400 = 20 (cm)
mà AM = 1212BC = 20 : 2 = 10 (cm) (AM là đường trung tuyến của tam giác ABC vuông tại A)
AN = MB (AMBN là hình thoi)
mà MB = MC (M là trung điểm của BC)
=> AN = MC
mà AN // MC (AMBN là hình thoi)
=> ACMN là hình bình hành
=> MN = AC
mà AC = 16 (cm)
=> MN = 16 (cm)

hình mình vẽ tượng trưng thôi nha
đề của bạn 1 số chỗ hơi nhầm đó nha.
a)
dựa theo công thức tính diện tích tam giác, ta có:
S\(\Delta\)ABC = \(\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
ta có:
AN = NC ; AM = MB
=> MN là đường trung bình của tam giác ABC
do đó MN//= \(\dfrac{1}{2}\)BC
=> MN = 6 cm
b) ta có:
AM = MB ; HM = ME
=> AHBE là hình bình hành
Mà ta lại thấy góc AHB vuông
=> AHBE là hình chữ nhật
c) ta có:
AH= HF ; CH = HB
=> ABFC là hình bình hành
Mà ta thấy AF \(\perp\) CB
suy ra ABFC là hình thoi.
d) mk k hỉu cái đề cho lắm nên thôi nha.![]()
chúc bạn học tốt

a: \(S_{ABC}=\dfrac{AH\cdot BC}{2}=12\cdot8=96\left(cm^2\right)\)
Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN=BC/2=6(cm)
b: Xét tứ giác AHBE có
M là trung điểm của AB
M là trung điểm của HE
Do đó:AHBE là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBE là hình chữ nhật
c: Xét tứ giác ABFC có
H là trung điểm của AF
H là trung điểm của BC
Do đó: ABFC là hình bình hành
mà AB=AC
nên ABFC là hình thoi
