TV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TL
30 tháng 6 2015
Gọi O là giao điểm của AC và BD
Do ABCD là hình thang cân và AC vuông BD nên ta có OCD là tam giác vuông cân tại O
=> Góc ODC = 450 => HDB vuông cân tại H
=> BH = DH
Dựng thêm đường cao AK.
Ta có ABHK là hình chữ nhật => HK = AB = 6
DK + HC = 2DK = DC - HK = 8 - 6 = 2 => 2DK = 2 => DK = 1
=> DH = DK + HK = 1 + 6 = 7 cm
Vậy BH = DH = 7cm.
31 tháng 7 2018
a, Bạn chứng minh được \(\Delta ABD\infty\Delta BDC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\Rightarrow AB.DC=BD^2\Rightarrow2.8=BD^2\Rightarrow BD^2=16\Rightarrow BD=4\left(cm\right)\)(vì AB = 2cm , CD = 8 cm)
Ta có: \(\frac{BD}{CD}=\frac{4}{8}=\frac{1}{2}\)
Xét tam giác BDC vuông tại B có: BD = 1/2 CD nên \(\widehat{C}=30^0\)
ABCD là hình thang vuông(gt) \(\Rightarrow AB//CD\)
\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\) ( 2 góc trong cùng phía)
\(\Rightarrow\widehat{ABC}+30^0=180^0\) (do góc C = 30 độ)
\(\Rightarrow\widehat{ABC}=150^0\)
b, Áp dụng định lí Pitago vào tam giác ABD vuông tại A, tính được: \(AD=\sqrt{12}\left(cm\right)\)
Diện tích hình thang ABCD là:
\(\frac{\left(2+8\right).\sqrt{12}}{2}=5\sqrt{12}\left(cm^2\right)\)
Chúc bạn học tốt.
CM
8 tháng 1 2017
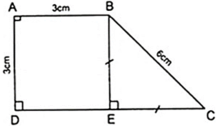
Xét hình thang cân ABCD ( AB//CD ) có Dˆ = 600
Theo định nghĩa và giả thiết về hình thang cân ta có: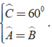 
Do góc A và góc D là hai góc cùng nằm một phía của
LD
29 tháng 3 2022
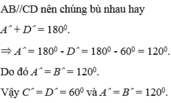
a, Xét ΔABD và ΔBDC có :
\(\widehat{A}=\widehat{DBC}\left(gt\right)\)
\(\widehat{ABD}=\widehat{BDC}\) (AB//CD, slt)
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(g-g\right)\)
b, Ta có : \(\Delta ABD\sim\Delta BDC\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BD}=\dfrac{AD}{DC}\)
hay \(\dfrac{6}{12}=\dfrac{8}{BC}\)
\(\Rightarrow BC=\dfrac{12.8}{6}=16\left(cm\right)\)
