Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta IHB\)có IA vừa là đường cao vừa là trung tuyến nên cân tại I, nên IA đồng thời là được phân giác
\(\Rightarrow\widehat{AIB}=\widehat{AIH}\)
Mà \(\widehat{AIH}=\widehat{DIC}\)( Đối đỉnh )
\(\Rightarrow\widehat{AIB}=\widehat{DIC}\)
Vậy ...

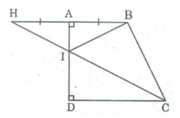
B và H đối xứng qua AD.
I và A đối xứng với chính nó qua AD
Nên ∠ (AIB) đối xứng với ∠ (AIH) qua AD
⇒ ∠ (AIB) = ∠ (AIH)
Lại có: ∠ (AIH) = ∠ (DIC) ( 2 góc đối đỉnh)
Suy ra: ∠ (AIB) = ∠ (DIC)

Hình tự vẽ nhé
Theo đề ra: K là điểm đối xứng của C qua AD <=> DC = DK
Xét hai tam giác vuông IDK và IDC:
+) DC = DK (cmt)
+) ID: chung
=> Tam giác IDK = IDC (Hai cạnh góc vuông)
=> Góc KID = CID
Ta có: AIB = KID (Đối đỉnh)
=> Góc AIB = góc CID

ủa bạn? mình làm không được mình mới gửi lên nhờ giúp, còn nói ảnh gì thì mình không biết

Xét ΔAIH và ΔAIB có: \(\left\{{}\begin{matrix}AH=BH\\\widehat{HAI}=\widehat{BAI}\\AI chung\end{matrix}\right.\)
=> ΔAIH = ΔAIB(c.g.c)
=> \(\widehat{AIH}=\widehat{AIB}\) (2 góc tương ứng) (1)
Mà \(\widehat{AIH}=\widehat{CID}\) (2 góc đối đỉnh)
=> \(\widehat{AIB}=\widehat{CID}\) (2)
Từ (1) và (2) =>đpcm
Xét ΔIAB vuông tại A và ΔIAH vuông tại A có
IA chung
AB=AH(gt)
Do đó: ΔIAB=ΔIAH(Hai cạnh góc vuông)
Suy ra: \(\widehat{AIB}=\widehat{AIH}\)(hai góc tương ứng)
mà \(\widehat{AIH}=\widehat{CID}\)(hai góc đối đỉnh)
nên \(\widehat{AIB}=\widehat{CID}\)

tự kẻ hình
a, có D đx D qua DI
I đx I qua DI
E đx C qua DI (gt)
=> tam giác EID = tam giác CID (đl)
=> góc IED = góc ICD (đn) (1)
AB // DC (gt) mà ABI slt IEC
=> góc ABI = góc IEC (đl) (2)
(1)(2) => góc ABI = góc ICD (tcbc)
có AIB + góc ABI = 90 do ...
góc CID + góc ICD = 90 do ...
góc IAB = IDC (gt)
=> góc AIB = góc CID
b, F đối xứng cái gì cơ
Hình bạn tự vẽ nhé
Xét Δ AIB và Δ AIH ta có
AH=AB(H đối xứng với B qua A)
Góc HAI= góc IAB(=900)
AI chung
Suy ra Δ AIB= Δ AIH(c-g-c)
Nên góc AIH = góc AIB (1)
Mà góc AIH= góc DIC(đối đỉnh) (2)
Từ (1) và (2) suy ra góc AIB= góc DIC