Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

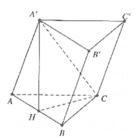
Đáp án C
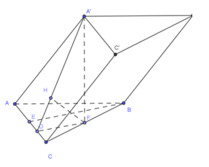
Gọi F là hình chiếu của A' lên mp (ABC), Nên góc A ' A F ^ là góc tạo bởi cạnh bên của AA' với (ABC), ⇒ A ' A F ^ = 30 0 ⇒ A F = A A ' cos 30 0 = 3 2 a ⇒
F là trung điểm của BC , gọi D,E là hình chiếu của F, B lên AC,H là hình chiếu của F lên AD. Dễ dàng chứng minh được FH là hình chiếu của F trên (ACC'A'), Ta có
d B , A C C ' A ' = 2 d F , A C C ' A ' = 2 F H .
A ' F = A A ' . c o s 30 0 = 1 2 a ; F D = 1 2 B E = 3 4 a
1 F H 2 = 1 A F 2 + 1 F D 2 ⇒ F H = a 21 7

Đáp án là A
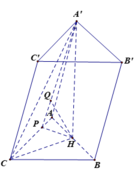

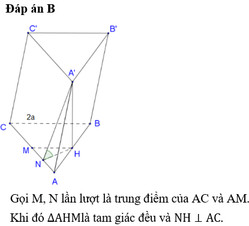
và AC bằng khoảng cách giữa B và (AA’C’C) và bằng 2 lần khoảng cách từ H tới (AA’C’C) và bằng 2HQ.



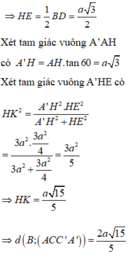

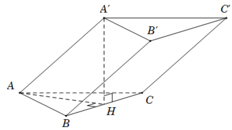


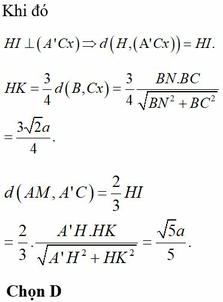
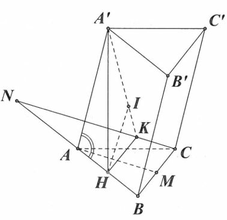
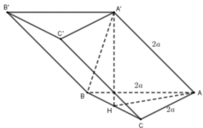


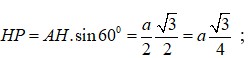
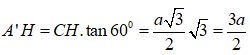
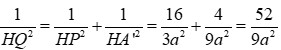
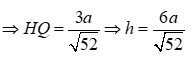
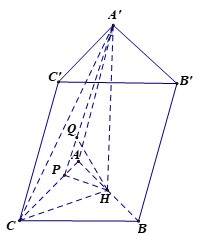
Đáp án B.
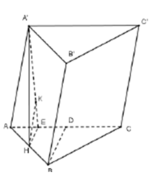
Do H là trung điểm AB nên d B ; A C C ' A ' d H ; A C C ' A ' = B A H A = 2
⇒ d B ; A C C ' A ' = 2 d d H ; A C C ' A '
Ta có A H ' ⊥ A B C nên A A ' , ( A B C ) ⏜ = A ' A , H A ⏜ = A ' A H ⏜ = 60 °
Gọi D là trung điểm của AC thì B D ⊥ A C .
Kẻ H E ⊥ A C , E ∈ A C → H E / / B D
Ta có A C ⊥ A ' H A C ⊥ H E ⇒ A C ⊥ A ' H E ⊥ A C C ' A '
Trong A ' H E kẻ H K ⊥ A ' E , K ∈ A ' E ⇒ H K ⊥ A C C ' A '
Suy ra
d H ; A C C ' A ' = H K ⇒ 2 d B ; A C C ' A ' = 2 H K
Ta có B D = 2 a 3 2 = a 3 ⇒ H E = 1 2 B D = a 3 2
Xét tam giác vuông A ' A H có A H ' = A H . tan 60 ° = a 3
Xét tam giác vuông A ' H E có 1 H K 2 = 1 A ' H 2 + 1 H E 2 = 1 a 3 2 + 1 a 3 2 2 = 5 3 a 2 ⇒ H K = a 15 5 .
Vậy d B ; A C C ' A ' = 2 H K = 2 a 15 5