Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
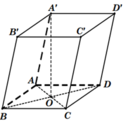
Gọi O = AC ∩ BD.Từ giả thiết suy ra A'O ⊥ ABCD
Cũng từ giả thiết, suy ra ABC là tam giác đều nên
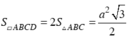
Đường cao khối hộp
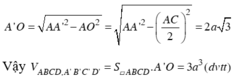

Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)

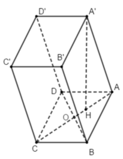
+ Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD
Ta có: A’B = A’D (đường chéo các hình thoi) ⇒ Tam giác A’BD cân tại A’ có O là trung điểm của BD ⇒ A’O ⊥ BD.
+ Hạ A’H ⊥ AC, H ∈ AC
Ta có B D ⊥ A C B D ⊥ A ' O ⇒ B D ⊥ A O A ' ⇒ A’H ⊥ BD
Do đó: A’H ⊥ (ABCD)
Vì (ABCD) // (A’B’C’D’) nên A’H chính là khoảng cách giữa hai mặt đáy.
+ Tính A’H
Ta có: AC = A D 2 + C D 2 − 2. A D . C D . cos 120 ° = a 3 ⇒ AO = a 3 2
Theo giả thiết ⇒ hình chóp A’.ABD là hình chóp đều, nên ta có:
AH = 2/3 AO = a 3 3
A’H = A ' A 2 − A H 2 = a 2 − a 2 3 = a 6 3
Vậy khoảng cách giữa hai đáy (ABCD) và (A’B’C’D’) là a 6 3 .
Đáp án B
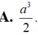
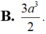
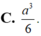
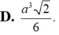



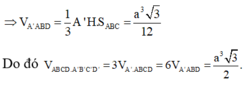
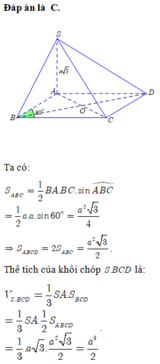
Đáp án C