ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

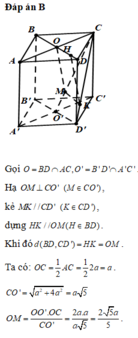
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
TT
Thái Thùy Linh
30 tháng 4 2021

Cho hình lăng trụ ABCD.A'B'C'D' đáy là hình vuông cạnh a, AA' = 2a . Khoảng cách giữa hai đường thẳng A'C và AB bằng
#Toán lớp 11
0
LA
Lan Anh
23 tháng 3 2023
Cho hình chóp S ABCD . có đáy ABCD là hình thoi cạnh 2a, SA a = 5 ; góc BCD = 60 o và SA vuông góc với ( ) ABCD . Gọi K là trung điểm của CD. Tính góc giữa đường thẳng SK và  ( SAB ).A. 450 .           B. 300 .           C. 600 .           D. arctan \(\dfrac{\sqrt{7}}{\sqrt{5}}\)help...
Đọc tiếp

Cho hình chóp S ABCD . có đáy ABCD là hình thoi cạnh 2a, SA a = 5 ; góc BCD = 60 o và SA vuông góc với ( ) ABCD . Gọi K là trung điểm của CD. Tính góc giữa đường thẳng SK và  ( SAB ).
A. 450 .           B. 300 .           C. 600 .           D. arctan \(\dfrac{\sqrt{7}}{\sqrt{5}}\)

help me


 
#Toán lớp 11
1
NL
Nguyễn Lê Phước Thịnh
23 tháng 3 2023

Chọn D

Đúng(0)
PT
Pham Trong Bach
16 tháng 3 2019
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB =2a, BC =a. Các cạnh bên của hình chóp bằng nhau và bằng a 2  . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là: A.  a 3 3 B.  a 6 3 C.  a 15 5   D.  a 21 7 ...
Đọc tiếp

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB =2a, BC =a. Các cạnh bên của hình chóp bằng nhau và bằng a 2  . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:

A.  a 3 3

B.  a 6 3

C.  a 15 5  

D.  a 21 7

#Toán lớp 11
1
CM
Cao Minh Tâm
16 tháng 3 2019

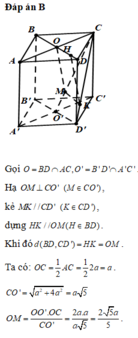
Đáp án D

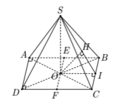
I  là trung điểm cạnh đáy BC. Do SA = SB = SC = SD nên SO ⊥  (ABCD)

Từ đó ta chứng minh được 

Tính được

 

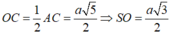
Suy ra

 

Đúng(0)
NP
Nguyễn Phúc
20 tháng 8 2019 - olm

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a AD=AA'=2a Khoảng cách giữa hai đường thẳng AC và DC' bằng

MIng mọi người giúp mình với 
#Toán lớp 11
0
LH
Lan Hương
4 tháng 4 2021

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=AA'=a, AC'=2a. Tìm đường vuông góc chung giữa AC' và CD', tính khoảng cách giữa chúng
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021

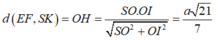
ABB'A' và CDD'C' là hình vuông \(\Rightarrow CD'\perp DC'\Rightarrow CD'\perp\left(ADC'B'\right)\)

Gọi M là giao điểm CD' và DC' \(\Rightarrow\) M là trung điểm 2 đoạn nói trên

Trong mp (ADC'B'), từ M kẻ \(MH\perp AC'\Rightarrow MH\) là đường vuông góc chung của AC' và CD'

\(DC'=AB'=\sqrt{AB^2+A'A^2}=a\sqrt{2}\)

\(\Rightarrow AD=B'C'=\sqrt{AC'^2-AB'^2}=a\sqrt{2}\)

\(\Rightarrow\Delta ADC'\) vuông cân tại D \(\Rightarrow\Delta MHC'\) vuông cân tại H

\(\Rightarrow MH=\dfrac{MC'}{\sqrt{2}}=\dfrac{DC'}{2\sqrt{2}}=\dfrac{a}{2}\)

Đúng(1)
PT
Phạm Thùy Dương
12 tháng 4 2019 - olm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 10. Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SC = 10√5. Gọi M,N lần lulư là trung điểm của SA và CD. Tính khoảng cách d giữa BD và MN.

A. d=3√5 

B. d=√5

C. d=5

D. d=10
#Toán lớp 11
4
S
_Shadow_
12 tháng 4 2019

Trả lời:

Đáp án B

~Học tốt~

Đúng(0)
NN
Nhóm Nhạc Thần Tượng
12 tháng 4 2019

Dap an B

đúng hay ko mk ko chắc

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP